设集合 ,集合
,集合 ,则集合B中元素的个数为( )
,则集合B中元素的个数为( )
| A.1 | B.2 | C.3 | D.4 |
下图是根据变量x,y的观测数据 得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是( )
得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是( )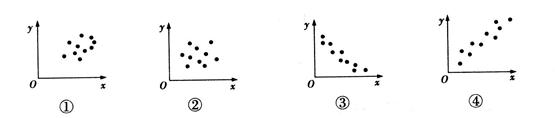
| A.①② | B.①④ | C.②③ | D.③④ |
①若“p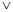 q”为真命题,则p、q均为真命题( );
q”为真命题,则p、q均为真命题( );
②“若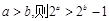 ”的否命题为“若
”的否命题为“若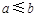 ,则
,则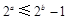 ”;
”;
③“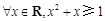 ”的否定是“
”的否定是“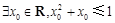 ”;
”;
④“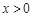 ”是“
”是“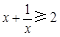 ”的充要条件. 其中不正确的命题是
”的充要条件. 其中不正确的命题是
| A.①② | B.②③ | C.①③ | D.③④ |
函数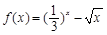 的零点所在区间为( )
的零点所在区间为( )
A.(0,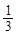 ) ) |
B.(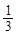 , , ) ) |
C.( ,1) ,1) |
D.(1,2) |
已知函数 的导函数
的导函数 的图象如图所示,则函数
的图象如图所示,则函数 的图象可能是( )
的图象可能是( )
A B C D
执行如图所示的程序框图,则输出的a的值为( )
A. |
B. |
C. |
D. |
已知平面直角坐标系xOy上的区域D由不等式组[来 给定. 若
给定. 若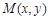 为D上的动点,点A的坐标为
为D上的动点,点A的坐标为 ,则
,则 的最大值为( )
的最大值为( )
| A.3 | B.4 | C.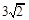 |
D. |
已知函数 ,在
,在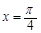 时取得极值,则函数
时取得极值,则函数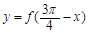 是( )
是( )
A.偶函数且图象关于点(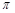 ,0)对称 ,0)对称 |
B.偶函数且图象关于点(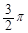 ,0)对称 ,0)对称 |
C.奇函数且图象关于点(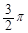 ,0)对称 ,0)对称 |
D.奇函数且图象关于点(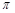 ,0)对称 ,0)对称 |
设平面向量 ,
, ,其中
,其中 记“使得
记“使得 成立的
成立的 ”为事件A,则事件A发生的概率为( )
”为事件A,则事件A发生的概率为( )
A. |
B. |
C. |
D. |
已知函数 是定义在R上的可导函数,其导函数记为
是定义在R上的可导函数,其导函数记为 ,若对于任意实数x,有
,若对于任意实数x,有 ,且
,且 为奇函数,则不等式
为奇函数,则不等式 的解集为( )
的解集为( )
A. |
B. |
C. |
D. |
若复数 ,其中i是虚数单位,则
,其中i是虚数单位,则 .
.
已知某一段公路限速60公里/小时,现抽取200辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这200辆汽车中在该路段没有超速的有 辆.
已知某几何体的三视图(单位cm)如图所示,则该几何体的体积为 cm3.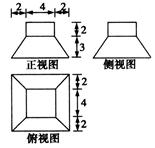
已知圆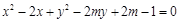 ,当圆的面积最小时,直线
,当圆的面积最小时,直线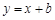 与圆相切,则
与圆相切,则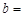 .
.
分别在区间[1,6]和[1,4]内任取一个实数,依次记为m和n,则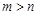 的概率为
的概率为
已知函数 . 若关于
. 若关于 的不等式
的不等式 的解集为空集,则实数
的解集为空集,则实数 的取值范围为 .
的取值范围为 .
观察如图三角形数阵,则
(1)若记第n行的第m个数为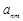 ,则
,则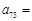 .
.
(2)第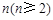 行的第2个数是 .
行的第2个数是 .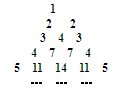
设函数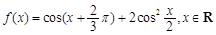 .
.
(1)求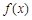 的值域;
的值域;
(2)记△ABC的内角A,B,C的对边长分别为a,b,c,若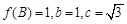 ,求a的值.
,求a的值.
已知数列 为等比数列,其前n项和为
为等比数列,其前n项和为 ,且满足
,且满足 ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)已知 ,记
,记 ,求数列
,求数列 前n项和
前n项和 .
.
如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, .
.
(1)求证 ,并指出异面直线PA与CD所成角的大小;
,并指出异面直线PA与CD所成角的大小;
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 ?如果存在,求出此时三棱锥
?如果存在,求出此时三棱锥 与四棱锥
与四棱锥 的体积比;如果不存在,请说明理由.
的体积比;如果不存在,请说明理由.
已知 ,函数
,函数 .
.
(Ⅰ)当 时,
时,
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若关于 的不等式
的不等式 在区间
在区间 上有解,求
上有解,求 的取值范围;
的取值范围;
(Ⅱ)已知曲线 在其图象上的两点
在其图象上的两点 ,
, (
( )处的切线分别为
)处的切线分别为 .若直线
.若直线 与
与 平行,试探究点
平行,试探究点 与点
与点 的关系,并证明你的结论.
的关系,并证明你的结论.
已知椭圆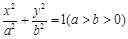 的离心率
的离心率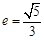 ,且直线
,且直线 是抛物线
是抛物线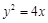 的一条切线.
的一条切线.
(1)求椭圆的方程;
(2)点P 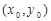 为椭圆上一点,直线
为椭圆上一点,直线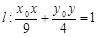 ,判断l与椭圆的位置关系并给出理由;
,判断l与椭圆的位置关系并给出理由;
(3)过椭圆上一点P作椭圆的切线交直线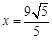 于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.