已知集合 ,
, ,则
,则 .
.
复数 (i是虚数单位)是纯虚数,则实数
(i是虚数单位)是纯虚数,则实数 的值为 .
的值为 .
一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出 人.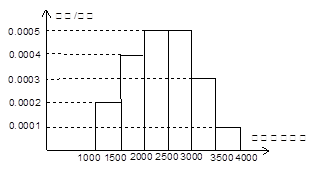
某算法的伪代码如图所示,若输出y的值为1,则输入 的值为 .
的值为 .
已知双曲线 的右焦点为
的右焦点为 ,则该双曲线的渐近线方程为________.
,则该双曲线的渐近线方程为________.
已知 ,则
,则 ________.
________.
已知正三棱柱底面边长是2,外接球的表面积是 ,则该三棱柱的侧棱长 .
,则该三棱柱的侧棱长 .
在R上定义运算⊙:a⊙b=ab+2a+b,则不等式x⊙(x-2)<0的解集是 .
投掷一枚正方体骰子(六个面上分别标有1,2,3,4,5,6),向上的面上的数字记为 ,又
,又 表示集合的元素个数,
表示集合的元素个数, ,则
,则 的概率为
的概率为
函数 的所有零点之和为 .
的所有零点之和为 .
如图, 是半径为1的圆
是半径为1的圆 的直径,△ABC是边长为1的正三角形,则
的直径,△ABC是边长为1的正三角形,则 的最大值为 .
的最大值为 .
已知数列 的首项
的首项 ,其前
,其前 项和为
项和为 ,且满足
,且满足 .若对任意的
.若对任意的 ,
, 恒成立,则
恒成立,则 的取值范围是 .
的取值范围是 .
已知圆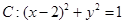 ,点
,点 在直线
在直线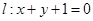 上,若过点
上,若过点 存在直线
存在直线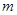 与圆
与圆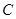 交于
交于 、
、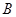 两点,且点
两点,且点 为
为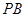 的中点,则点
的中点,则点 横坐标
横坐标 的取值范围是 .
的取值范围是 .
记实数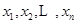 中的最大数为
中的最大数为 ,最小数为
,最小数为 .已知实数
.已知实数 且三数能构成三角形的三边长,若
且三数能构成三角形的三边长,若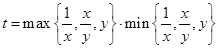 ,则
,则 的取值范围是 .
的取值范围是 .
已知函数 (
( ),其图像在
),其图像在 处的切线方程为
处的切线方程为 .函数
.函数 ,
, .
.
(1)求实数 、
、 的值;
的值;
(2)以函数 图像上一点为圆心,2为半径作圆
图像上一点为圆心,2为半径作圆 ,若圆
,若圆 上存在两个不同的点到原点
上存在两个不同的点到原点 的距离为1,求
的距离为1,求 的取值范围;
的取值范围;
(3)求最大的正整数 ,对于任意的
,对于任意的 ,存在实数
,存在实数 、
、 满足
满足 ,使得
,使得 .
.
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.求AM的长;
已知二阶矩阵M有特征值 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成
变换成 ,求矩阵M。
,求矩阵M。
已知曲线 的极坐标方程是
的极坐标方程是 ,直线的参数方程是
,直线的参数方程是 (为参数).
(为参数).
设直线与 轴的交点是
轴的交点是 ,
, 是曲线
是曲线 上一动点,求
上一动点,求 的最大值.
的最大值.
已知 ,且
,且 ,求
,求 的最小值.
的最小值.
如图, 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,
=1, =2,又
=2,又 =1,∠
=1,∠ =120°,
=120°, ⊥
⊥ ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°.
(1)求二面角 的的余弦值;
的的余弦值;
(2)求点 到面
到面 的距离.
的距离.
已知二项式 的展开式中第2项为常数项
的展开式中第2项为常数项 ,其中
,其中 ,且展开式按
,且展开式按 的降幂排列.
的降幂排列.
(1)求 及
及 的值.
的值.
(2)数列 中,
中, ,
, ,
, ,求证:
,求证: 能被4整除.
能被4整除.