已知复数z满足 ,则z =( )
,则z =( )
A. |
B. |
C. |
D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. |
B. |
C.(0,1) | D.(1,0) |
已知定义在复数集 上的函数
上的函数 满足
满足 ,则
,则 等于 ( )
等于 ( )
A. |
B. |
C. |
D. |
已知函数 ,其导函数
,其导函数 的部分图象如图所示,则函数
的部分图象如图所示,则函数 的解析式为( )
的解析式为( )
A. |
B. |
C. |
D. |
下列命题中是假命题的是( )
A. 上递减 上递减 |
B. |
C. |
D. 都不是偶函数 都不是偶函数 |
已知 是两条不重合的直线,
是两条不重合的直线, 是三个不重合的平面,则
是三个不重合的平面,则 的一个充分条件是( )
的一个充分条件是( )
A. |
B. |
C. |
D. 是异面直线, 是异面直线, |
已知某程序框图如图所示,则该程序运行后输出的结果为 ( )
A. |
B. |
C. |
D. |
从星期一到星期六安排甲、乙、丙三人值班,每人值2天班,如果甲不安排在星期一,乙不安排在星期六,那么值班方案种数为( )
| A.42 | B.30 | C.72 | D.60 |
已知函数 的定义域为
的定义域为 ,当
,当 时,
时, ,且对任意的
,且对任意的 ,等式
,等式 成立,若数列
成立,若数列 满足
满足 ,且
,且 则
则 的值为( )
的值为( )
| A.4016 | B.4017 | C.4018 | D.4019 |
已知圆 :
: ,过圆
,过圆 内定点P(2,1)作两条相互垂直的弦AC和BD,那么四边形ABCD面积最大值为( )
内定点P(2,1)作两条相互垂直的弦AC和BD,那么四边形ABCD面积最大值为( )
| A.21 | B. |
C. |
D.42 |
若 展开式的二项式系数之和为256,则
展开式的二项式系数之和为256,则 =_________,其展开式的常数项等于__________。(用数字作答)
=_________,其展开式的常数项等于__________。(用数字作答)
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 cm3.
已知 满足
满足 且目标函数
且目标函数 的最大值为7,最小值为1,
的最大值为7,最小值为1,
则 。
。
在 中,
中, ,O为
,O为 的内心,且
的内心,且 则
则 = .
= .
已知 内接于椭圆
内接于椭圆 ,且
,且 的重心G落在坐标原点O,则
的重心G落在坐标原点O,则 的面积等于 .
的面积等于 .
函数 的值域为 .
的值域为 .
已知函数 ,其定义域为
,其定义域为 ,最大值为6.
,最大值为6.
(1)求常数m的值;
(2)求函数 的单调递增区间.
的单调递增区间.
袋中装有若干个质地均匀大小一致的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球然后放回,若累计3次摸到红球则停止摸球,否则继续摸球直至第5次摸球后结束.
(1)求摸球3次就停止的事件发生的概率;
(2)记摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及其期望.
的分布列及其期望.
如图,已知四棱锥 的底面的菱形,
的底面的菱形, ,点
,点 是
是 边的中点,
边的中点, 交于点
交于点 ,
,

(1)求证: ;
;
(2)若 的大小;
的大小;
(3)在(2)的条件下,求异面直线 与
与 所成角的余弦值。
所成角的余弦值。
已知椭圆C的两个焦点分别为 ,且点
,且点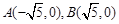 在椭圆C上,又
在椭圆C上,又 .
.
(1)求焦点F2的轨迹 的方程;
的方程;
(2)若直线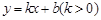 与曲线
与曲线 交于M、N两点,以MN为直径的圆经过原点,求实数b的取值范围.
交于M、N两点,以MN为直径的圆经过原点,求实数b的取值范围.
已知函数
(1)若方程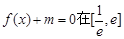 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
(2)如果函数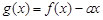 的图象与x轴交于两点
的图象与x轴交于两点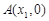 、
、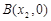 且
且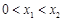 .求证:
.求证: (其中正常数
(其中正常数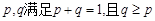 ).
).
已知数列 满足:
满足: 其中
其中 ,数列
,数列 满足:
满足:
(1)求 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在正数k,使得数列 的每一项均为整数,如果不存在,说明理由,如果存在,求出所有的k.
的每一项均为整数,如果不存在,说明理由,如果存在,求出所有的k.