已知全集 ,集合
,集合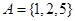 ,
,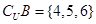 ,则
,则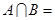 ( )
( )
A.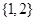 |
B.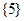 |
C.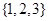 |
D.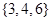 |
抛物线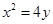 的焦点坐标是( )
的焦点坐标是( )
A.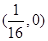 |
B.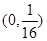 |
C.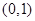 |
D. |
已知定义在复数集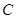 上的函数
上的函数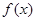 满足
满足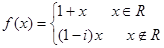 ,则
,则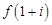 等于( )
等于( )
A.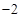 |
B.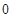 |
C.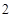 |
D.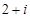 |
已知两个平面 、
、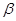 ,直线
,直线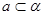 ,则“
,则“ ”是“直线
”是“直线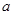
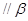 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知函数
 的部分图象如图所示,则函数
的部分图象如图所示,则函数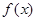 的解析式为( )
的解析式为( )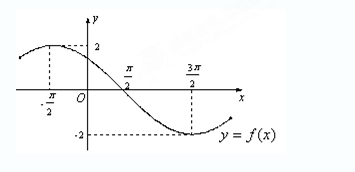
A.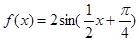 |
B.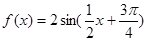 |
C.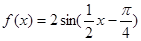 |
D.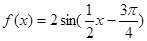 |
下列命题中是假命题的是( )
A.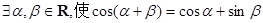 ; ; |
B.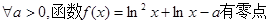 |
C.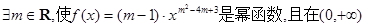 上递减 上递减 |
D.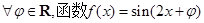 都不是偶函数 都不是偶函数 |
已知某程序框图如图所示,则该程序运行后输出的结果为( )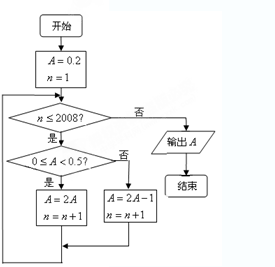
A.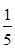 |
B.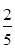 |
C.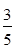 |
D.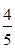 |
已知点A(3,0),B(0,3),C(cosα,sinα),O(0,0),若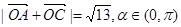 ,则
,则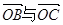 的夹角为( )
的夹角为( )
A.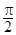 |
B. |
C.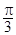 |
D. |
已知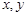 满足
满足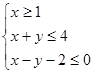 ,记目标函数
,记目标函数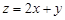 的最大值为
的最大值为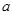 ,最小值为
,最小值为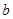 ,则
,则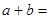
A.1 B.2 C.7 D.8
定义在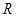 上的函数
上的函数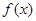 满足
满足 ,当
,当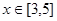 时
时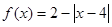 ,则( )
,则( )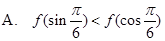
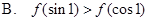
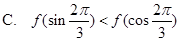
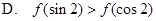
已知双曲线的右焦点为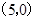 ,一条渐近线方程为
,一条渐近线方程为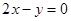 ,则此双曲线的标准方程是 .
,则此双曲线的标准方程是 .
有四条线段长度分别为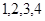 ,从这四条线段中任取三条,则所取三条线段能构成三角形的概率为 .
,从这四条线段中任取三条,则所取三条线段能构成三角形的概率为 .
若过点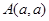 可作圆
可作圆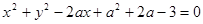 的两条切线,则实数
的两条切线,则实数 的取值范围为 .
的取值范围为 .
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 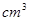 .
.
设向量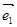 和
和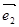 是夹角为
是夹角为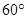 的两个单位向量,则向量
的两个单位向量,则向量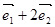 的模为 .
的模为 .
已知数组: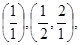
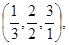
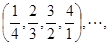
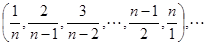 记该数组为:
记该数组为: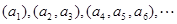 ,则
,则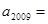 .
.
已知关于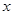 的一元二次函数
的一元二次函数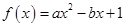 ,设集合
,设集合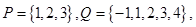 ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为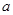 和
和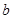
(1)求函数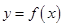 有零点的概率;
有零点的概率;
(2)求函数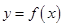 在区间
在区间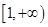 上是增函数的概率。
上是增函数的概率。
已知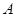 ,
,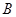 ,
,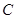 是三角形
是三角形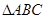 三内角,向量
三内角,向量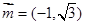 ,
,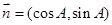 ,且
,且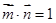 .
.
⑴求角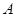 ;
;
⑵若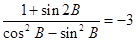 ,求
,求 .
.
如图,已知 为平行四边形,
为平行四边形,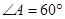 ,
,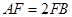 ,
, ,点
,点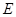 在
在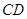 上,
上,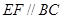 ,
,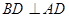 ,
,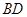 与
与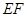 相交于
相交于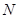 .现将四边形
.现将四边形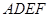 沿
沿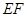 折起,使点
折起,使点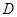 在平面
在平面 上的射影恰在直线
上的射影恰在直线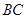 上.
上.
(1)求证: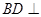 平面
平面 ;
;
(2)求折后直线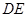 与平面
与平面 所成角的余弦值.
所成角的余弦值.
已知数列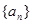 的前
的前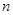 项和
项和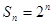 ,数列
,数列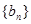 满足
满足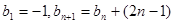
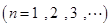 .
.
(1)求数列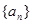 的通项
的通项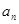 ;
;
(2)求数列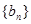 的通项
的通项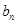 ;
;
(3)若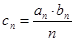 ,求数列
,求数列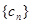 的前
的前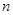 项和
项和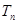 .
.
已知函数 (
( )
)
(1)若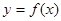 在点
在点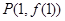 处的切线方程为
处的切线方程为 ,求
,求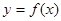 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)若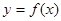 在
在 上存在极值点,求实数
上存在极值点,求实数 的取值范围.
的取值范围.
已知椭圆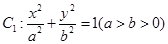 的长轴长为
的长轴长为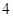 ,离心率为
,离心率为 ,
,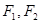 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点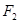 ,且与直线
,且与直线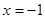 相切.
相切.
(1)(ⅰ)求椭圆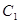 的方程;(ⅱ)求动圆圆心轨迹
的方程;(ⅱ)求动圆圆心轨迹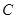 的方程;
的方程;
(2)在曲线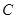 上有四个不同的点
上有四个不同的点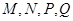 ,满足
,满足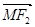 与
与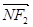 共线,
共线,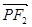 与
与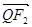 共线,且
共线,且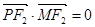 ,求四边形
,求四边形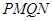 面积的最小值.
面积的最小值.