已知 为虚数单位,复数
为虚数单位,复数 的虚部是( )
的虚部是( )
A. |
B. |
C. |
D. |
重庆市教委为配合教育部公布高考改革新方案,拟定在重庆 中学进行调研,广泛征求高三年级学生的意见。重庆
中学进行调研,广泛征求高三年级学生的意见。重庆 中学高三年级共有700名学生,其中理科生500人,文科生200人,现采用分层抽样的方法从中抽取14名学生参加调研,则抽取的理科生的人数为( )
中学高三年级共有700名学生,其中理科生500人,文科生200人,现采用分层抽样的方法从中抽取14名学生参加调研,则抽取的理科生的人数为( )
| A.2 | B.4 | C.5 | D.10 |
下列函数中,既是偶函数,又在区间 上是减函数的是( )
上是减函数的是( )
A. |
B. |
C. |
D. |
设集合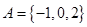 ,集合
,集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若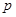 是
是 的必要条件,
的必要条件, 是
是 的充分条件,那么下列推理一定正确的是( )
的充分条件,那么下列推理一定正确的是( )
A. |
B. |
C. |
D. |
执行如图所示的程序框图,则输出的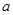 为( )
为( )
| A.20 | B.14 | C.10 | D.7 |
某几何体的三视图如题(6)所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为( )
| A.1 | B. |
C. |
D. |
设 是椭圆
是椭圆 上两点,点
上两点,点 关于
关于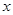 轴的对称点为
轴的对称点为 (异于点
(异于点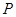 ),若直线
),若直线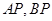 分别交
分别交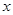 轴于点
轴于点 ,则
,则 ( )
( )
| A.0 | B.1 | C. |
D.2 |
对任意实数 ,定义运算
,定义运算 :
: ,设
,设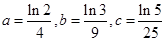 ,则
,则 的值是( )
的值是( )
A. |
B. |
C. |
D.不确定 |
已知 中,
中, 边的中点,过点
边的中点,过点 的直线分别交直线
的直线分别交直线 、
、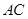 于点
于点 、
、 ,若
,若 ,
, ,其中
,其中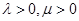 ,则
,则 的最小值是( )
的最小值是( )
| A.1 | B. |
C. |
D. |
已知 ,且
,且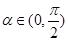 ,则
,则 .
.
若正项等比数列 满足:
满足: ,则公比
,则公比 .
.
已知函数 的导函数为
的导函数为 ,若
,若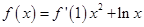 ,则
,则 .
.
若关于 的不等式
的不等式 的解集为
的解集为 ,则关于
,则关于 的不等式
的不等式 的解集为 .
的解集为 .
在已知平面区域 ,直线
,直线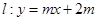 和曲线
和曲线 有两个不同的交点,直线
有两个不同的交点,直线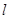 与曲线
与曲线 围成的平面区域为
围成的平面区域为 ,向区域
,向区域 内随机投一点
内随机投一点 ,点
,点 落在区域
落在区域 内的概率为
内的概率为 ,若
,若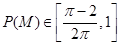 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为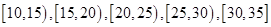 ,得到如题(16)图所示的频率分布直方图。已知生产的产品数量在
,得到如题(16)图所示的频率分布直方图。已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(1)求 ;
;
(2)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,求这2位工人不在同一组的概率.
已知向量 ,函数
,函数 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)设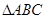 的三边
的三边 、
、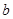 、
、 满足:
满足: ,且边
,且边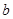 所对的角为
所对的角为 ,若关于
,若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
设 为等差数列
为等差数列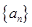 的前
的前 项和,已知
项和,已知 .
.
(1)求 ;
;
(2)设 ,数列
,数列 的前
的前 项和记为
项和记为 ,求证:
,求证: .
.
已知直四棱柱 的底面
的底面 为正方形,
为正方形, ,
, 为棱
为棱 的中点.
的中点.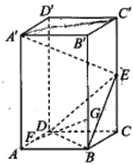
(1)求证: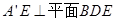 ;
;
(2)设 为
为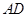 中点,
中点, 为棱
为棱 上一点,且
上一点,且 ,求证:
,求证: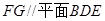 .
.
已知函数 .
.
(1)若函数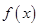 在
在 内单调递增,求
内单调递增,求 的取值范围;
的取值范围;
(2)若函数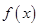 在
在 处取得极小值,求
处取得极小值,求 的取值范围.
的取值范围.
如图所示,离心率为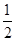 的椭圆
的椭圆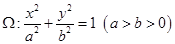 上的点到其左焦点的距离的最大值为3,过椭圆
上的点到其左焦点的距离的最大值为3,过椭圆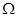 内一点
内一点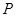 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点 、
、 和
和 、
、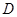 ,且满足
,且满足 ,其中
,其中 为常数,过点
为常数,过点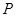 作
作 的平行线交椭圆于
的平行线交椭圆于 、
、 两点.
两点.
(1)求椭圆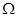 的方程;
的方程;
(2)若点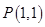 ,求直线
,求直线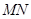 的方程,并证明点
的方程,并证明点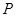 平分线段
平分线段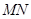 .
.