以下给出的是计算 的值的一个程序框图(如图所示),其中
的值的一个程序框图(如图所示),其中
判断框内应填入的条件是 ( )
| A. i>10 | B. i<10 | C. i<20 | D. i>20 |
一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,测得平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为 ,那么
,那么 的值为
的值为
| A.5 | B.6 | C.7 | D.8 |
某初级中学领导采用系统抽样方法 ,从该校预备年级全体800名学生中抽50名
,从该校预备年级全体800名学生中抽50名
学生做牙齿健康检查。 现将800名学生从1到800进行编号,求得间隔数k
现将800名学生从1到800进行编号,求得间隔数k =16,即
=16,即
每16人抽取 一个人。在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个
一个人。在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个
数中应取的数是 ( )
A. 40 40 |
B.39 |
C.38 |
D.37 |
从一箱产品 中随机地抽取一件,设事件A={抽到一等品},事件B ={抽到二等品},事件C ={抽到三等品},且已知P(A)=" 0.65" ,P(B)="0.2" ,P(C)=0.1。则事件“抽到的不是一等品”的概率为 ( )
中随机地抽取一件,设事件A={抽到一等品},事件B ={抽到二等品},事件C ={抽到三等品},且已知P(A)=" 0.65" ,P(B)="0.2" ,P(C)=0.1。则事件“抽到的不是一等品”的概率为 ( )
A.0.7 B.0.65 C.0.35  D.0.3
D.0.3
设 ,
, ,且
,且
 ,则锐角
,则锐角 为 ( )
为 ( )
A. |
B. |
C. |
D. |
如图,在直角坐标系 中,射线
中,射线 交单位圆
交单位圆 于点
于点 ,若
,若 ,则
,则
点 的坐标是 ( )
的坐标是 ( )
A. |
B.  |
C. |
D. |
若函数 (ω>0)在区间
(ω>0)在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,则
上单调递减,则 ( )
( )
A. |
B. |
C.2 | D.3 |
某产品的广告费用x与销售额y的统计数据如下表
根据上表可得回归方程 中的
中的 为9.4,据此模型预报广告费用为
为9.4,据此模型预报广告费用为
6万元时销售额为 ( )
| A.63.6万元 | B.65.5万元 | C.67.7万元 | D.72.0万元 |
要得到函数 的图象,只需要将
的图象,只需要将 的图象 ( ).
的图象 ( ).
A.向右平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向左平移 个单位 个单位 |
在区间 上随机取一个数
上随机取一个数 ,使
,使 的值介于
的值介于 到1之间的概率为 ( )
到1之间的概率为 ( )
A. |
B. |
C. |
D. |
在 中,点P是AB上一点,且
中,点P是AB上一点,且 , Q是BC中点,AQ与
, Q是BC中点,AQ与
CP交点为M,又 ,则
,则 的值为 ( )
的值为 ( )
A. |
B. |
C. |
D. |
设 分别是
分别是 轴,
轴, 轴正方向上的单位向量,
轴正方向上的单位向量, ,
, 。若用α来表示
。若用α来表示 与
与 的夹角,则α等于( )
的夹角,则α等于( )
A. |
B. |
C. |
D. |
已知A(2,3), ,点P在线段BA延长线上,
,点P在线段BA延长线上, 且
且 ,
,
则点P的坐标是________.
设f(sina+cosa)=sina•cosa,则f(sin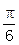 )的值为______.
)的值为______.
若 =(2,1),
=(2,1), =(-3,-4),则向量
=(-3,-4),则向量 在向量
在向量 方向上的正射影的坐标___________.
方向上的正射影的坐标___________.
 ________
________ _______。
_______。
(本小题满分10分)
有两颗正四面体的玩具,其四个面上分别标有数字1,2,3,4,下面做投掷这两颗正四面体玩具的试验:用 表示结果,其中
表示结果,其中 表示投掷第1颗正四面体玩具落在底面的数字,
表示投掷第1颗正四面体玩具落在底面的数字, 表示投掷第2颗正四面体玩具落在底面的数字。
表示投掷第2颗正四面体玩具落在底面的数字。
(1)写出试验的基本事件;
(2)求事件“落在底面的数字之和大于3”的概率;
(3)求事件“落在底面的数字相等”的概率。
(本小题满分12分)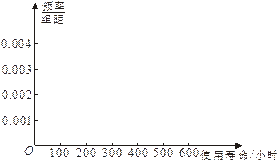
对某电子元件进行寿命追踪调查,情况如下:
| 寿命/小时 |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)完成频率分布表;
| 分组 |
频数 |
频率 |
| 100~200 |
|
|
| 200~300 |
|
|
| 300~400 |
|
|
| 400~500 |
|
|
| 500~600 |
|
|
| 合计 |
|
|
(2)画出频率分布直方图和频率分布折线图;
(3)估计电子元件寿命在100~400小时以内的频率;
(本小题满分12分)
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤ )的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若
)的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若 ,求函数y=2sin(πx+φ)的最值,及取得最值时
,求函数y=2sin(πx+φ)的最值,及取得最值时 的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求
的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求 的余弦值。
的余弦值。
(本小题满分12分)
设向量
 ,其中
,其中 .
.
(1)求 的取值范围;
的取值范围;
(2)若函数 的大小
的大小
(本小题满分12分)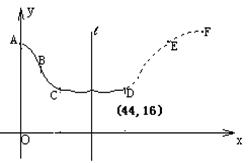
在股票市场上,投资者常参考股价(每一股的价格)的某 条平滑均线(记作MA)的变化情况来决定买入或卖出股票。股民老赵在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式
条平滑均线(记作MA)的变化情况来决定买入或卖出股票。股民老赵在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式
 来描述,从C点走到今天的D点,是震荡筑底阶段,而今
来描述,从C点走到今天的D点,是震荡筑底阶段,而今 天出现了明显的
天出现了明显的 筑底结束的标志,且D点和C
筑底结束的标志,且D点和C 点正
点正 好关于直线
好关于直线 对称。老赵预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线
对称。老赵预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线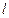 对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。现在老赵决定取点
对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。现在老赵决定取点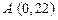 ,点
,点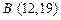 ,点
,点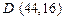 来确定解析式中的常数
来确定解析式中的常数 ,并且已经求得
,并且已经求得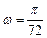 。
。
(1)请你帮老赵算出
 ,并回答股价什么时候见顶(即求F点的横坐标);
,并回答股价什么时候见顶(即求F点的横坐标);
(2)老赵如能在今天以D点处的价格买入该股票5000股,到见顶处F点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
(本小题满分12分)
已知函数 ,
, ,(
,( )
)
(1)问 取何值时,方程
取何值时,方程 在
在 上有两解;
上有两解;
(2)若对任意的 ,总存在
,总存在 ,使
,使 成立,求实数
成立,求实数 的取值范围?
的取值范围?