已知集合 ,集合
,集合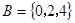 ,则
,则 等于
等于
A. |
B. |
C. |
D. |
若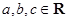 ,且
,且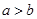 ,则下列不等式中恒成立的是
,则下列不等式中恒成立的是
A. |
B. |
C. |
D.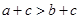 |
函数 的图象可能是 ( )
的图象可能是 ( )
已知条件 ,条件
,条件 ,则
,则 是
是
 成立的 ( )
成立的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
幂函数 的图象过点
的图象过点 ,那么函数
,那么函数 的单调递增区间是
的单调递增区间是
A. |
B. |
C. |
D. |
若函数 为偶函数,则函数
为偶函数,则函数 的一条对称轴是
的一条对称轴是
A. |
B. |
C. |
D. |
已知集合 ,且
,且 ,则实数
,则实数 的取值范围是
的取值范围是
A. |
B. |
C. |
D. |
若曲线 在点P处的切线平行于直线
在点P处的切线平行于直线 ,则点P的坐标为
,则点P的坐标为
| A.(-1,2) | B.(1,-3) | C.(1,0) | D.(1,5) |
若函数 的一个正数零点附近的函数值用二分法计算,其参
的一个正数零点附近的函数值用二分法计算,其参
考数据如下:
| f (1) = -2 |
f (1.5) = 0.625 |
f (1.25) =" " -0.984 |
| f (1.375) =" " -0.260 |
f (1.4375) = 0.162 |
f (1.40625) = -0.054 |
那么方程 的一个近似根(精确到0.1)为
的一个近似根(精确到0.1)为
A.1.2 B.1.3 C.1.4 D.1.5
若偶函数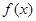 满足
满足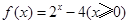 ,则不等式
,则不等式 的解集是
的解集是
A.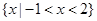 |
B.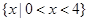 |
C. |
D.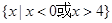 |
函数 ,若函数
,若函数 有3个零点,则实数
有3个零点,则实数 的
的
值为
| A.-4 | B.-2 | C.2 | D.4 |
设函数 是定义在R上周期为3的奇函数,若
是定义在R上周期为3的奇函数,若 ,则有
,则有
A. 且 且 |
B. 或 或 |
C. |
D. |
曲线 在点
在点 处的切线方程为 .
处的切线方程为 .
在平面直角坐标系 中, 二元一次方程
中, 二元一次方程 (
( 不同时为
不同时为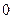 )表示过原点的直线. 类似地: 在空间直角坐标系
)表示过原点的直线. 类似地: 在空间直角坐标系 中, 三元一次方程
中, 三元一次方程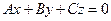 (
( 不同时为
不同时为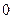 )表示 .
)表示 .
设不等式组 所表示的平面区域是一个三角形,则此平面区域面积的最大值 .
所表示的平面区域是一个三角形,则此平面区域面积的最大值 .
函数 的单调递减区间 .
的单调递减区间 .
(本小题满分12分)设命题 :实数
:实数 满足
满足 ,
, 实数
实数 满足
满足 ,若
,若 为真,求实数
为真,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 的导数
的导数 满足
满足 ,
, ,其中常数
,其中常数 ,求曲线
,求曲线 在点
在点 处的切线方程.
处的切线方程.
(本小题满分12分)
已知函数 是
是 上的奇函数,且单调递减,解关于
上的奇函数,且单调递减,解关于 的不等式
的不等式 ,其中
,其中 且
且 .
.
(本小题满分12分)已知 ,证明:
,证明: .
.
(本小题满分12分)
某玩具厂计划每天生产A、B、C三种玩具共100个. 已知生产一个玩具A需5分钟,生产一个玩具B需7分钟,生产一个玩具C需4分钟,而且总生产时间不超过10个小时. 若每生产一个玩具A、B、C可获得的利润分别为5元、6元、3元.
(I)用每天生产的玩具A的个数 与玩具B的个数
与玩具B的个数 表示每天的利润
表示每天的利润 元;
元;
(II)请你为玩具厂制定合理的生产任务分配计划,使每天的利润最大,并求最大利润.
(本小题满分14分)
某光学仪器厂有一条价值为 万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值
万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值 万元与技术改造投入
万元与技术改造投入 万元之间满足:①
万元之间满足:① 与
与 成正比;②当
成正比;②当 时,
时, ,并且技术改造投入满足
,并且技术改造投入满足 ,其中
,其中 为常数且
为常数且 .
.
(I)求 表达式及定义域;
表达式及定义域;
(II)求技术改造之后,产品增加值的最大值及相应 的值.
的值.