若1和
的等差中项是2，则的值为( ）
| A．4 | B．3 | C．1 | D． |
计算
的结果为( ）
A． |
B． |
C． |
D． |
在△ABC中，
，
，
，则
等于( ）
A． |
B． |
C． |
D． |
已知函数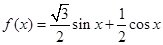
在
处取得最大值，则可能是( ）
A． |
B． |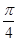
C． |
D． |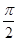
等比数列
的首项为1，其前
项和为
，如果
，则
的值为 ( ）
| A．2 | B．2或 |
C．4 | D．4或 |
数列
的通项公式为
，其前
项和为
，则
的值为 ( ）
A． |
B． |
C． |
D． |
等差数列
满足
，且前10项和
，则
最大值是 ( ）
| A．28 | B．49 | C．50 | D．52 |
若在△ABC中，有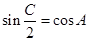
，则△ABC一定是 ( ）
| A．锐角三角形 | B．钝角三角形 | C．直角三角形 | D．等腰三角形 |
在△ABC中，
，
，
，则△ABC的面积为 .
若角
的终边经过点
，则
，
.
已知等差数列
的前
项和为
，若
，且
，则的公差是 ，的最小值为 .
已知在△ABC中，有
，则下列说法中：①△ABC为钝角三角形；②
；③
.
正确说法的序号是 .（填上所有正确说法的序号）
设数列
满足
，若
，则
= ，
数列的前10项和
= .
已知
，定义
.
（1）如果
，则
；
（2）如果
，则
的取值范围是 .
已知函数
.
（1）求
值；
（2）求
的最小值正周期；
（3）求的单调递增区间.
已知等差数列
满足
.
（1）求的通项公式；
（2）求的前
项和
；
（3）若
成等比数列，求
的值.
已知△ABC中，
，
,且
.
（1）求∠B的值；
（2）若点E,P分别在边AB,BC上，且AE=4，AP⊥CE，求AP的长；
已知数列
中，
，且有
.
（1）写出
所有可能的值；
（2）是否存在一个数列满足：对于任意正整数
，都有
成立？若有，请写出这个数列的前6项，若没有，说明理由；
（3）求
的最小值.