已知集合 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
“实数 ”是“复数
”是“复数 (
( 为虚数单位)的模为
为虚数单位)的模为 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分条件又不必要条件 |
数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D. |
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
| A.48cm3 | B.98cm3 | C.88cm3 | D.78cm3 |

执行如图所示的程序框图,输出的S值为( )
A. |
B. |
C. |
D. |
已知 ,函数
,函数 在
在 上单调递减.则
上单调递减.则 的取值范围是 ( )
的取值范围是 ( )
A. |
B. |
C. |
D. |
函数 的部分图像如图所示,则
的部分图像如图所示,则 的解析式可以是( )
的解析式可以是( )
A. |
B. |
C. |
D. |
从编号为001,002, ,500的500个产品中用系统抽样的方法抽取一个样本,已知样本中编号最小的两个编号分别为007,032,则样本中最大的编号应该为
| A.480 | B.481 | C.482 | D.483 |
偶函数 满足
满足 ,且在
,且在 时,
时, ,则关于
,则关于 的方程
的方程 在
在 上的根的个数是
上的根的个数是
| A.3 | B.4 | C.5 | D.6 |
已知 ,
, 是双曲线
是双曲线 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点 与点
与点 关于直线
关于直线 对称,则该双曲线的离心率为
对称,则该双曲线的离心率为
A. |
B. |
C. |
D. |
某公司一年购买某种货物400吨,每次都购买 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则 ___ ____ 吨.
___ ____ 吨.
设 ,若
,若 ,则实数
,则实数 的值为 .
的值为 .
已知 ,
, 满足约束条件
满足约束条件 ,且
,且 的最小值为6,则常数
的最小值为6,则常数 .
.
已知直角梯形ABCD, ,
, ,
, ,沿
,沿 折叠成三棱锥,当三棱锥体积最大时,三棱锥外接球的体积为 .
折叠成三棱锥,当三棱锥体积最大时,三棱锥外接球的体积为 .
如图,在正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧上的任意一点,设向量 .
.
在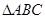 中,角
中,角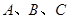 所对的边为
所对的边为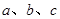 ,且满足
,且满足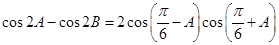
(1)求角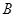 的值;
的值;
(2)若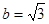 且
且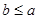 ,求
,求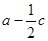 的取值范围.
的取值范围.
在对某渔业产品的质量调研中,从甲,乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).
下表是测量数据的茎叶图:
规定:当产品中的此种元素含量 毫克时为优质品.
毫克时为优质品.
(1)试用上述样本数据估计甲,乙两地该产品的优质品率(优质品件数/总件数);
(2)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数 的分布列及数学期望
的分布列及数学期望 .
.
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B—PC—D的大小为 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
设数列 为等差数列,且
为等差数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,
, 且
且 .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若 ,
, 为数列
为数列 的前
的前 项和,
项和, 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.
如图,已知椭圆 ,直线
,直线 的方程为
的方程为 ,过右焦点
,过右焦点 的直线
的直线 与椭圆交于异于左顶点
与椭圆交于异于左顶点 的
的 两点,直线
两点,直线 ,
, 交直线
交直线 分别于点
分别于点 ,
, .
.
(1)当 时,求此时直线
时,求此时直线 的方程;
的方程;
(2)试问 ,
, 两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.
两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.
设函数 .
.
(1)若函数 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值;
(2)若存在 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.