设集合
，
,
,则
．
已知复数
满足
（
为虚数单位），则
.
命题“若
，则
（
R）”否命题的真假性为 （从“真”、“假”中选填一个）．
已知集合
，若
，
，则
的值等于 .
若
是纯虚数，则实数
的值是 .
“
”，“
”，若
是
的充分不必要条件，则
的取值范围是 ．
函数
的单调减区间为___________.
曲线
在点
处的切线方程是 ．
若命题“
，使
”的否定是假命题，则实数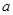
的取值范围是 .
设函数
是定义在
上的偶函数，当
时，
，若
，则实数
的值为 .
已知函数
(
)的图像如图所示，则不等式
的解集为________．
已知
是定义在
上的函数，且对任意实数
，恒有
，且的最大值为1，则不等式
的解集为 .
求“方程
的解”有如下解题思路：设
，则
在
上单调递减，且
，所以原方程有唯一解
．类比上述解题思路，方程
的解为 ．
已知函数
若
，使得
成立，则实数
的取值范围是 ．
已知集合
，
.
（1）当
时，求
；
（2）若
，求实数
的取值范围.
设
：
，
：关于
的不等式
的解集是空集，试确定实数
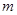的取值范围，使得或为真命题，且为假命题.
复数
＝
且
，对应的点在第一象限，若复数
对应的点是正三角形的三个顶点，求实数
的值．
(1）用综合法证明：
(
)
（2）用反证法证明：若
均为实数，且
，
，
求证：中至少有一个大于0.
已知函数
．
（1）若函数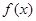
在
上是增函数，求实数
的取值范围；
（2）若函数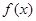在
上的最小值为3，求实数的值．
已知函数
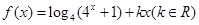为偶函数．
(1)求
的值；
(2)若方程
有且只有一个根，求实数
的取值范围．