设集合 ,
, ,若
,若 ,则
,则 的值为( )
的值为( )
A. |
B.1 | C. |
D.0 |
复数 为虚数单位)的共轭复数在复平面上对应的点的坐标是 ( )
为虚数单位)的共轭复数在复平面上对应的点的坐标是 ( )
A. |
B. |
C. |
D. |
已知命题p、q,“ 为真”是“p
为真”是“p 为假”的( )
为假”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 ,若
,若 ,
,
则 ( )
( )
| A.-1 | B.0 | C.l | D.256 |
如图, 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为( )
| A.1 | B.2 | C.3 | D.4 |

已知函数 ,则使函数
,则使函数 有零点的实数
有零点的实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
如果执行如图所示的程序框图,则输出的结果S为( )
| A.0 | B. |
C. |
D. |

设 其中实数
其中实数 满足
满足 ,若
,若 的最大值为
的最大值为 ,则
,则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
函数
 的部分图象如图所示,为了得到
的部分图象如图所示,为了得到 的图象,只需将
的图象,只需将 的图象( )
的图象( )
A.向右平移 个单位 个单位 |
B.向左平移 个单位 个单位 |
C.向右平移 个单位 个单位 |
D.向左平移 个单位 个单位 |

在边长为1的正三角形ABC中, =x
=x ,
, =y
=y ,x>0,y>0,且x+y=1,则
,x>0,y>0,且x+y=1,则 ·
· 的最大值为 ( )
的最大值为 ( )
A.- |
B.- |
C.- |
D.- |
设 是双曲线
是双曲线 的两个焦点,
的两个焦点, 是
是 上一点,
上一点, ,
, 的最小内角为
的最小内角为 ,则曲线
,则曲线 的离心率为( )
的离心率为( )
A. |
B. |
C.2 | D. |
已知函数 ,若
,若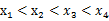 ,
,
且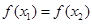
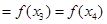 ,则
,则 ( )
( )
| A.2 | B.4 | C.8 | D.随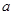 值变化 值变化 |
为了解某市甲、乙、丙三所学校高三数学模拟考试成绩,采取分层抽样方法,从甲校的1260份试卷、乙校的720份试卷、丙校的900份试卷中进行抽样调研.如果从丙校的900份试卷中抽取了45份试卷,那么这次调研共抽查的试卷份数为___________ .
已知直线 与圆
与圆 交于
交于 、
、 两点,
两点, 是原点,C是圆上一点,若
是原点,C是圆上一点,若 ,则
,则 的值为_______ .
的值为_______ .
设A、B、C、D是半径为2的球面上的四点,且满足 ,
, 的最大值是 _______ .
的最大值是 _______ .
在△ABC中,设AD为BC边上的高,且AD = BC,b,c分别表示角B,C所对的边长,则 的取值范围是_______ .
的取值范围是_______ .
数列 的前
的前 项和为
项和为 ,且
,且 是
是 和
和 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
在如图的几何体中,四边形 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形, ∥
∥ ,
, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
某地为迎接2014年索契冬奥会,举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛,其得分情况如茎叶图所示:
(1)若从甲运动员的不低于80且不高于90的得分中任选3个,求其中与平均得分之差的绝对值不超过2的概率;
(2)若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个,求甲、乙两名运动员得分之差的绝对值 的分布列与期望.
的分布列与期望.
设椭圆C1: =1(a>b>0)的左、右焦点分别为为
=1(a>b>0)的左、右焦点分别为为 ,
, 恰是抛物线C2:
恰是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
的焦点,点M为C1与C2在第一象限的交点,且|MF2|= .
.
(1)求C1的方程;
(2)平面上的点N满足 ,直线l∥MN,且与C1交于A,B两点,若
,直线l∥MN,且与C1交于A,B两点,若 ,求直线l的方程.
,求直线l的方程.
已知函数 .
.
(1)讨论函数 在
在 上的单调性;
上的单调性;
(2)当 时,曲线
时,曲线 上总存在相异两点,
上总存在相异两点, ,
, ,使得
,使得 曲线在
曲线在 、
、 处的切线互相平行,求证:
处的切线互相平行,求证: .
.
如图,在 中,
中, 是的∠A的平分线,圆
是的∠A的平分线,圆 经过点
经过点 与
与 切于点
切于点 ,与
,与 相交于
相交于 ,连结
,连结 ,
, .
.
(1)求证: ; (2)求证:
; (2)求证: .
.
已知曲线 (
( 为参数),曲线
为参数),曲线 ,将
,将 的横坐标伸长为原来的2倍,纵坐标缩短为原来的
的横坐标伸长为原来的2倍,纵坐标缩短为原来的 得到曲线
得到曲线 .
.
(1)求曲线 的普通方程,曲线
的普通方程,曲线 的直角坐标方程;
的直角坐标方程;
(2)若点P为曲线 上的任意一点,Q为曲线
上的任意一点,Q为曲线 上的任意一点,求线段
上的任意一点,求线段 的最小值,并求此时的P的坐标.
的最小值,并求此时的P的坐标.
已知函数 (a是常数,a∈R)
(a是常数,a∈R)
(1)当a=1时求不等式 的解集.
的解集.
(2)如果函数 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.