设 是虚数单位,那么复数
是虚数单位,那么复数 等于( )
等于( )
A.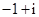 |
B. |
C. |
D. |
已知集合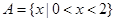 ,
, ,则
,则 为( )
为( )
A. |
B.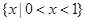 |
C. |
D. |
观察下列关于变量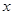 和
和 的三个散点图,它们从左到右的对应关系依次是( )
的三个散点图,它们从左到右的对应关系依次是( )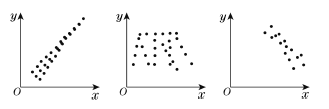
| A.正相关、负相关、不相关 | B.负相关、不相关、正相关 |
| C.负相关、正相关、不相关 | D.正相关、不相关、负相关 |
命题:“ ,都有
,都有 ”的否定是( )
”的否定是( )
A. ,都有 ,都有 |
B. ,都有 ,都有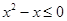 |
C. ,使得 ,使得 |
D.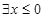 ,使得 ,使得 |
函数 的单调递增区间是 ( )
的单调递增区间是 ( )
A. |
B. |
C.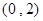 |
D.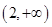 |
某程序框图如图所示,若输入 ,则该程序运行后输出的
,则该程序运行后输出的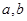 值分别是( )
值分别是( )
A. |
B.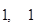 |
C.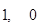 |
D. |

直线 与圆
与圆 相交所得线段的长度为 ( )
相交所得线段的长度为 ( )
A. |
B. |
C. |
D. |
某几何体的三视图如右图所示,则该几何体的表面积是( )
A. |
B. |
C. |
D. |
若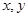 均为区间
均为区间 的随机数,则
的随机数,则 的概率为( )
的概率为( )
A. |
B. |
C. |
D.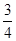 |

对于函数 在定义域内的任意实数
在定义域内的任意实数 及
及 ,都有
,都有 及
及 成立,则称函数
成立,则称函数 为“
为“ 函数”.现给出下列四个函数:
函数”.现给出下列四个函数:

 ;
; .其中是“
.其中是“ 函数”的是( )
函数”的是( )
A.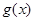 |
B. |
C. |
D.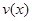 |
在边长为2的等边 中,
中, 是
是 的中点,
的中点, 为线段
为线段 上一动点,则
上一动点,则 的取值范
的取值范
围是( )
A. |
B.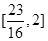 |
C. |
D.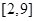 |
设函数 的导函数为
的导函数为 ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A.若 ,则 ,则 是函数 是函数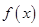 的极值点 的极值点 |
B.若 是函数 是函数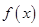 的极值点,则 的极值点,则 |
C.若 是函数 是函数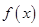 的极值点,则 的极值点,则 可能不存在 可能不存在 |
D.若 无实根 ,则函数 无实根 ,则函数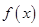 必无极值点 必无极值点 |
在等差数列 中,若
中,若 ,则
,则 .
.
已知椭圆的焦点是双曲线的顶点,双曲线的焦点是椭圆的长轴顶点,若两曲线的离心率分别为 则
则 ______.
______.
已知 若直线
若直线 与直线
与直线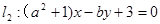 互相垂直,则
互相垂直,则 的
的
最小值是 .
定义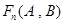 表示所有满足
表示所有满足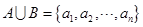 的集合
的集合 组成的有序集合对
组成的有序集合对 的个数.试探究
的个数.试探究 ,并归纳推得
,并归纳推得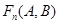 =_________.
=_________.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6.
(1)估计所抽取的数学成绩的众数;
(2)用分层抽样的方法在成绩为 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在 恰有1人的概率.
恰有1人的概率.
将数列 按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
个数 构成公差为
构成公差为 的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为
的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为 的等比数列.若
的等比数列.若 ,
, ,
, .
.
(1)求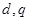 的值;
的值;
(2)求第 行各数的和
行各数的和 .
.
如图,在三棱锥 中,平面
中,平面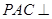 平面
平面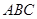 ,
,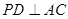 于点
于点 ,且
,且 ,
, ,
,
(1)求证:
(2)
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
(已知抛物线 (
( )的准线与
)的准线与 轴交于点
轴交于点 .
.
(1)求抛物线的方程,并写出焦点坐标;
(2)是否存在过焦点的直线 (直线与抛物线交于点
(直线与抛物线交于点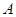 ,
, ),使得三角形
),使得三角形 的面积
的面积 ?若存在,请求出直线
?若存在,请求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
设向量
 ,定义一种向量积
,定义一种向量积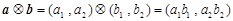 .
.
已知向量 ,
,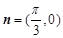 ,点
,点 为
为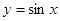 的图象上的动点,点
的图象上的动点,点
为 的图象上的动点,且满足
的图象上的动点,且满足 (其中
(其中 为坐标原点).
为坐标原点).
(1)请用 表示
表示 ;
;
(2)求 的表达式并求它的周期;
的表达式并求它的周期;
(3)把函数 图象上各点的横坐标缩小为原来的
图象上各点的横坐标缩小为原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数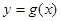 的图象.设函数
的图象.设函数
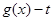
 ,试讨论函数
,试讨论函数 在区间
在区间 内的零点个数.
内的零点个数.
已知函数
 为自然对数的底数).
为自然对数的底数).
(1)求曲线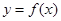 在
在 处的切线方程;
处的切线方程;
(2)若 是
是 的一个极值点,且点
的一个极值点,且点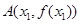 ,
,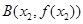 满足条件:
满足条件: .
.
(ⅰ)求 的值;
的值;
(ⅱ)求证:点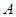 ,
,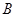 ,
, 是三个不同的点,且构成直角三角形.
是三个不同的点,且构成直角三角形.