已知 是虚数单位,则复数
是虚数单位,则复数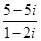 等于 ( )
等于 ( )
A.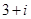 |
B.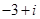 |
C.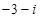 |
D. |
已知集合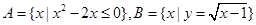 ,则
,则 ( )
( )
A.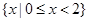 |
B. |
C.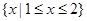 |
D.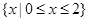 |
已知函数 则
则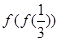 的值为( )
的值为( )
A.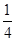 |
B.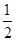 |
C. |
D.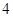 |
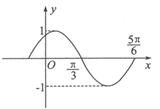
如图所示,是函数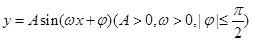 图象的一部分.则
图象的一部分.则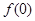 的值为( )
的值为( )
A.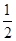 |
B.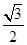 |
C.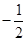 |
D.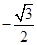 |
如图是一个算法的流程图.若输入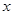 的值为
的值为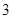 ,则输出
,则输出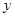 的值是( )
的值是( )
A.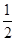 |
B.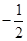 |
C.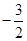 |
D.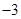 |
进入4月份,天气渐暖,蔬菜上市品种逐渐增加.某蔬菜销售市场,根据连续5周的市场调研,对某种蔬菜的销售量 (千克)与价格
(千克)与价格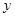 (元∕千克)统计数据(如表所示)表明:二者负相关,其回归方程为
(元∕千克)统计数据(如表所示)表明:二者负相关,其回归方程为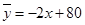 ,则统计表格中的实数
,则统计表格中的实数 的值为( )
的值为( )
| 周次 |
1 |
2 |
3 |
4 |
5 |
销售量 |
18 |
19 |
18 |
22 |
23 |
价格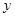 |
45 |
43 |
 |
35 |
33 |
A.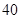 B.
B.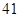 C.
C.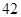 D.
D.
已知直线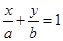 与圆
与圆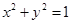 没有公共点,则 ( )
没有公共点,则 ( )
A. |
B.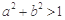 |
C.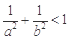 |
D.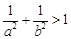 |
已知  为
为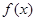 的导函数,则
的导函数,则 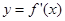 的图象大致是( )
的图象大致是( )

下列命题正确的有( )个?
①命题“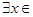 R使得
R使得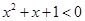 ”的否定是:“
”的否定是:“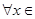 R均有
R均有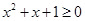 ”.
”.
②若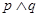 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
③若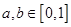 ,则不等式
,则不等式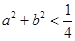 成立的概率是
成立的概率是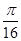 ;
;
④“平面向量 与
与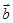 的夹角是钝角”的充分不必要条件是“
的夹角是钝角”的充分不必要条件是“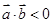 ”.
”.
| A.1 | B.2 | C.3 | D.4 |
已知定义在实数集 上的偶函数
上的偶函数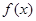 满足
满足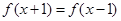 ,且当
,且当 时,
时,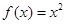 ,则关于
,则关于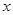 的方程
的方程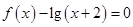 在
在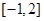 上实根的个数是( )
上实根的个数是( )
A.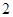 |
B.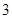 |
C.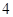 |
D.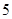 |
已知一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图均为正方形,那么该几何体的体积是 .
已知实数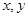 满足:
满足: ,则
,则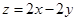 的最小值为 .
的最小值为 .
等差数列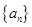 满足:
满足: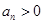 ,且前
,且前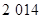 项和
项和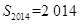 ,则
,则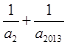 的最小值为________.
的最小值为________.
已知直线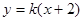 (k>0)与抛物线
(k>0)与抛物线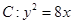 相交于
相交于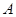 、
、 两点,
两点,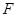 为
为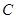 的焦点,若
的焦点,若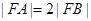 ,则k的值为 .
,则k的值为 .
给出以下四个命题:
①为了解600名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑用系统抽样,则分段的间隔k为30;
②已知 是空间四点,命题甲:
是空间四点,命题甲: 四点不共面,命题乙:直线
四点不共面,命题乙:直线 和
和 不相交,则甲是乙成立的充分不必要条件;
不相交,则甲是乙成立的充分不必要条件;
③对分类变量X与Y的随机变量k2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.
④若双曲线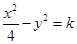 的渐近线方程为
的渐近线方程为 ,则k=1.其中真命题的序号是 .
,则k=1.其中真命题的序号是 .
已知向量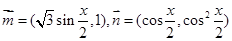 .记
.记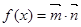
(I)求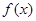 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(Ⅱ)在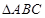 中,角
中,角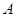 ,
,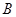 ,
,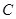 的对边分别为
的对边分别为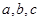 若
若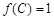 ,
,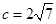 ,
,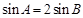 ,求
,求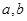 的值.
的值.
(本小题满分12分)如图,在三棱柱 中,
中,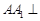 底面
底面 ,
,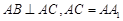 ,E、F分别是棱
,E、F分别是棱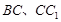 的中点.
的中点.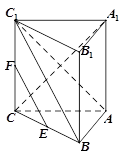
(Ⅰ)求证:AB⊥平面AA1 C1C;
(Ⅱ)若线段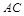 上的点
上的点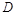 满足平面
满足平面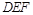 //平面
//平面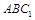 ,试确定点
,试确定点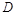 的位置,并说明理由;
的位置,并说明理由;
(本小题满分12分)对某社区青年志愿者参加社区服务次数统计,随机抽去了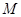 名志愿者作为样本,得到这
名志愿者作为样本,得到这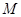 名志愿者参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名志愿者参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
| 分组 |
频数 |
频率 |
 |
9 |
0.45 |
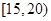 |
5 |
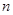 |
 |
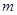 |
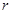 |
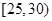 |
2 |
0.1 |
| 合计 |
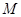 |
1 |
(Ⅰ)求出表中 的值;
的值;
(Ⅱ)在所取样本中,从参加社区服务的次数不少于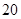 次的志愿者中任选
次的志愿者中任选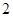 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间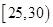 内的概率.
内的概率.
已知数列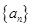 为等差数列,且
为等差数列,且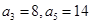 ,数列
,数列 的前
的前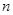 项和为
项和为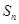 ,
,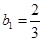 且
且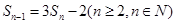
(Ⅰ)求数列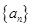 ,
, 的通项公式;
的通项公式;
(Ⅱ)若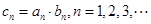 ,求数列
,求数列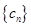 的前
的前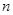 项和
项和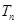 .
.
(本小题满分13分)已知函数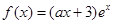 (
( ),其中
),其中 自然对数的底数。
自然对数的底数。
(1)若函数图象在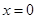 处的切线方程为
处的切线方程为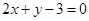 ,求
,求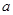 的值;
的值;
(2)求函数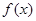 的单调区间;
的单调区间;
(3)设函数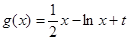 ,当
,当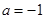 时,存在
时,存在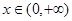 使得
使得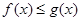 成立,求
成立,求 的取值范围.
的取值范围.
已知椭圆
 的两个焦点分别为
的两个焦点分别为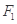 ,
,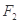 ,离心率为
,离心率为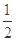 ,过
,过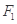 的直线
的直线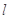 与椭圆
与椭圆 交于
交于 两点,且
两点,且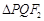 的周长为
的周长为 .
.
(I)求椭圆 的方程;
的方程;
(Ⅱ)过原点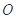 的两条互相垂直的射线与椭圆
的两条互相垂直的射线与椭圆 分别交于
分别交于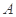 ,
,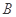 两点,求证:点
两点,求证:点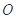 到直线
到直线 的距离为定值,并求出这个定值.
的距离为定值,并求出这个定值.