函数 的最小正周期为
的最小正周期为 .
.
函数 的反函数为_______.
的反函数为_______.
已知集合 ,
, ,则
,则 =_____
=_____
已知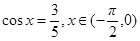 ,则
,则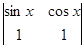 =_______
=_______
 的展开式中
的展开式中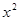 的系数为_____________.(用数字作答)
的系数为_____________.(用数字作答)
设 是虚数单位,复数
是虚数单位,复数 为方程
为方程 的一个根,则
的一个根,则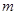 =________.
=________.
从4名男同学和3名女同学中随机选出3人参加演讲比赛,则女同学被抽到的数学期望为________.
某圆锥体的侧面展开图是半圆,当侧面积是 时,则该圆锥体的体积是 .
时,则该圆锥体的体积是 .
已知 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 , 则
, 则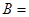 ______
______
极坐标系中, 分别是直线
分别是直线 和圆
和圆 上的动点,则
上的动点,则 两点之间距离的最小值是
两点之间距离的最小值是
对于正项数列 ,定义
,定义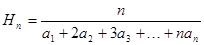 为
为 的“光阴”值,现知某数列的“光阴”值为
的“光阴”值,现知某数列的“光阴”值为 ,则数列
,则数列 的通项公式为________
的通项公式为________
过点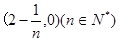 且方向向量为
且方向向量为 的直线交椭圆
的直线交椭圆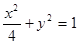 于
于 两点,记原点为
两点,记原点为 ,
, 面积为
面积为 ,则
,则 _______
_______
将正整数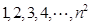 (
( )任意排成
)任意排成 行
行 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数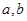 (
(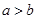 )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.若
,称这些比值中的最小值为这个数表的“特征值”.若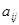 表示某个
表示某个 行
行 列数表中第
列数表中第 行第
行第 列的数(
列的数( ,
, ),且满足
),且满足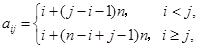 ,当
,当 时数表的“特征值”为_________
时数表的“特征值”为_________
如图,在直角梯形 中,
中, ,
,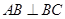 ,
, ,
,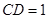 ,
, ,P为线段
,P为线段 (含端点)上一个动点,设
(含端点)上一个动点,设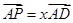 ,
,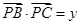 ,对于函数
,对于函数 ,给出以下三个结论:①当
,给出以下三个结论:①当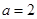 时,函数
时,函数 的值域为
的值域为 ;②对任意
;②对任意 ,都有
,都有 成立;③对任意
成立;③对任意 ,函数
,函数 的最大值都等于4.④存在实数
的最大值都等于4.④存在实数 ,使得函数
,使得函数 最小值为0 .其中所有正确结论的序号是_________.
最小值为0 .其中所有正确结论的序号是_________.
执行如图所示的程序框图.若输入 ,则输出
,则输出 的值是( )
的值是( )
A. |
B.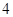 |
C. |
D. |
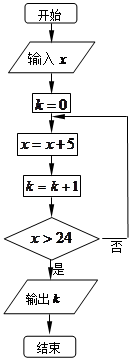
某高中学校采用系统抽样方法,从该校全体800名学生中抽50名学生做牙齿健康检查.现将800名学生从1到800进行编号,求得间隔数k =16,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33 ~ 48这16个数中应取的数是( )
=16,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33 ~ 48这16个数中应取的数是( )
| A.40 | B.39 | C.38 | D.37 |
已知 为双曲线
为双曲线 的左右焦点,点
的左右焦点,点 在
在 上,
上,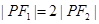 ,则
,则 ( )
( )
A.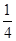 |
B. |
C. |
D. |
函数 的定义域为
的定义域为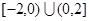 ,其图像上任一点
,其图像上任一点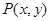 都位于椭圆
都位于椭圆 :
: 上,下列判断①函数
上,下列判断①函数 一定是偶函数;②函数
一定是偶函数;②函数 可能既不是偶函数,也不是奇函数;③函数
可能既不是偶函数,也不是奇函数;③函数 可能是奇函数;④函数
可能是奇函数;④函数 如果是偶函数,则值域是
如果是偶函数,则值域是 ;⑤函数
;⑤函数 值域是
值域是 ,则一定是奇函数.其中正确的命题个数有( )个
,则一定是奇函数.其中正确的命题个数有( )个
| A.1 | B.2 | C.3 | D.4 |
如图,直三棱柱 中,
中,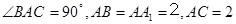 ,
, 为
为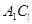 中点,求直线
中点,求直线 与平面
与平面 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)
如图,某污水处理厂要在一正方形污水处理池 内修建一个三角形隔离区以投放净化物质,其形状为三角形
内修建一个三角形隔离区以投放净化物质,其形状为三角形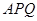 ,其中
,其中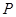 位于边
位于边 上,
上, 位于边
位于边 上.已知
上.已知 米,
米,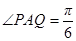 ,设
,设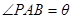 ,记
,记 ,当
,当 越大,则污水净化效果越好.
越大,则污水净化效果越好.
(1)求 关于的函数解析式,并求定义域;
关于的函数解析式,并求定义域;
(2)求 最大值,并指出等号成立条件?
最大值,并指出等号成立条件?
数列 的首项
的首项 ,
,
求数列 的通项公式;
的通项公式;
设 的前
的前 项和为
项和为 ,若
,若 的最小值为
的最小值为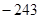 ,求
,求 的取值范围?
的取值范围?
在平面直角坐标系 中,原点为
中,原点为 ,抛物线
,抛物线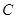 的方程为
的方程为 ,线段
,线段 是抛物线
是抛物线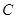 的一条动弦.
的一条动弦.
(1)求抛物线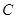 的准线方程和焦点坐标
的准线方程和焦点坐标 ;
;
(2)若 ,求证:直线
,求证:直线 恒过定点;
恒过定点;
(3)当 时,设圆
时,设圆 ,若存在且仅存在两条动弦
,若存在且仅存在两条动弦 ,满足直线
,满足直线 与圆
与圆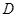 相切,求半径
相切,求半径 的取值范围?
的取值范围?
定义函数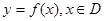 (
( 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的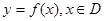 的模.若模存在最大值,则称之为函数
的模.若模存在最大值,则称之为函数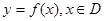 的长距;若模存在最小值,则称之为函数
的长距;若模存在最小值,则称之为函数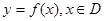 的短距.
的短距.
(1)分别判断函数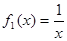 与
与 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;
(2)求证:指数函数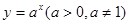 的短距小于1;
的短距小于1;
(3)对于任意 是否存在实数
是否存在实数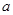 ,使得函数
,使得函数 的短距不小于2且长距不大于4.若存在,请求出
的短距不小于2且长距不大于4.若存在,请求出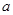 的取值范围;不存在,则说明理由?
的取值范围;不存在,则说明理由?