下列两个变量之间是相关关系的是( )
| A．圆的面积与半径 | B．球的体积与半径 |
| C．角度与它的正弦值 | D．一个考生的数学成绩与物理成绩 |
根据右边程序框图，当输入10时，输出的是（ ）
| A．12 | B．19 | C．14.1 | D．-30 |
的值为 （ ）
.
.1 
.
. 
用反证法证明命题：“若a,b∈N，ab能被3整除，那么a,b
中至少有一个能被3整除”时，假设应为（ ）
| A．a、b都能被3整除 | B．a、b都不能被3整除 |
| C．a、b不都能被3整除 | D．a不能被3整除 |
已知x与y之间的一组数据：
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程为
必过（ ）
A．点
B．点
C．点
D．点
若
是实系数方程
的一个根，则方程的另一根为（ ）
A． |
B． |
C． |
D． |
点
，则它的极坐标是（ ）
A． |
B． |
C． |
D． |
若x＞4，则函数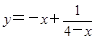
（ ）
| A．有最大值—6 | B．有最小值6 | C．有最大值—2 | D．有最小值2 |
不等式
的解集为 （ ）
A．（ ，1）∪（1， ） |
B．（－∞，）∪（，+∞） |
| C．（－∞，1）∪（，+∞） |
D．（，1）∪（，+∞） |
在平面里，有勾股定理：“设△ABC的两边AB．AC互相垂直，则
拓展到空间，类比平面几何的勾股定理．研究三棱锥的侧面积与底面面积问的关系。可以得出的正确结论是：“设三棱锥A—BCD的三个侧面△ABC．△ACD．△ADB两两相互垂直，则____________________
不等式 
>
，对一切实数
都成立，则实 数的取值范围是
直线
的斜率为
极坐标方程
化为直角坐标方程是
本小题满分12分）
已知复数
，若
（1）求
； （2）求实数
的值
（本小题满分12分）
打鼾不仅影响别人休息，而且可能与患某种疾病有关，下表是一次调查所得数据，试问：每一晚都打鼾与患心脏病有关系吗？有多大把握认为你的结论成立？
| |
患心脏病 |
未患心脏病 |
合计 |
| 每一晚都打鼾 |
46 |
30 |
76 |
| 不打鼾 |
20 |
50 |
70 |
| 合计 |
66 |
80 |
146 |
（本小题满分12分）
的极坐标方程分别为
（Ⅰ）把的极坐标方程化为直角坐标方程
（Ⅱ）求经过交点的直线的直角坐标方程
（本小题满分13分）
如图，过抛物线
（
＞0）的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k，试用k表示点A、B的坐标
⑵求弦AB中点M的轨迹方程
（本小题满分12分）
围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位：元)。（Ⅰ）将总费用y表示为x的函数
（Ⅱ）试确定x,使修建此矩形场地围墙的总费用最小，并求出最小总费用
复数
等于 （ ）
| A．-i | B．i | C．1 | D．-1 |
（本小题满分14分）
如右图所示的三角形数阵叫“莱布尼兹调和三角形“，它们是由整数的倒数组成的，第n行有n个数且两端的数均为
（n≥２），其余每个数是它下一行左右相邻两个数的和，如： 
．．．．．．，则第7行第4个数（从左往右数）为 