设集合
，
，则（ ）
A． |
B． |
C． |
D． |
若复数z满足
，则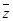
=（ ）
A． |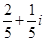
B． |
C． |
D． |
已知
，
，
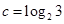，则（ ）
A． |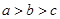
B． |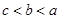
C． |
D． |
在等比数列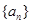
中，
，
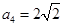，则
（ ）
A． |
B． |
C．8 | D．4 |
函数
的一段大致图象是（ ）
椭圆
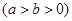的左、右焦点为
，过
作直线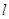
交C于A，B两点，若
是等腰直角三角形，且
，则椭圆C的离心率为（ ）
A． |
B． |
C． |
D． |
执行左下面的程序框图，如果输入的依次为3,5,3,5,4,4,3,4,4，则输出的S为（ ）
A． |
B．4 | C． |
D． |
右上图是某几何体的三视图，则该几何体的体积等于（ ）
| A．1 | B． |
C． |
D． |
三棱锥
的四个顶点都在球面上，SA是球的直径，
，
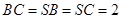，则该球的表面积为（ ）
A． |
B． |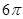
C． |
D． |
中，D是BC中点，
，
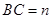，则
等于（ ）
A． |
B． |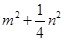
C． |
D． |
若
，且
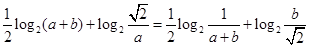，则
（ ）
| A．0 | B． |
C．1 | D．2 |
函数
的最大值为（ ）
A． |
B．2 | C． |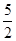
D． |
曲线
在
处的切线方程为 .
以双曲线
的上焦点为圆心，与该双曲线的渐近线相切的圆的方程为 .
观察等式：
，
，
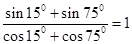.照此规律，对于一般的角
，有等式 .
设数列
满足
，
，
，则数列的前n项和为 .
如图，正三角形ABC的边长为2，D，E，F分别在三边AB，BC和CA上，且D为AB的中点，
，
，
.
（1）当
时，求
的大小；
（2）求
的面积S的最小值及使得S取最小值时的值.
在斜三棱柱
中，平面
平面ABC，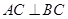
，
，
.
（1）求证：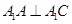
；
（2）若
，求三棱锥
的体积.
为了了解高一年级学生的身高情况，某校按10%的比例对全校800名高一年级学生按性别进行抽样检查，得到如下频数分布表：
表1：男生身高频数分布表
| 身高（cm） |
[160,165） |
[165,170） |
[170,175） |
[175,180） |
[180,185） |
[185,190] |
| 频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2：男生身高频数分布表
| 身高（cm） |
[150,155） |
[150,160） |
[160,165） |
[165,170） |
[170,175） |
[175,180] |
| 频数 |
2 |
12 |
16 |
6 |
3 |
1 |
（1）分别估计高一年级男生和女生的平均身高；
（2）在样本中，从身高180cm以上的男生中任选2人，求至少有一人身高在185cm以上的概率.
过抛物线C：
上的点M分别向C的准线和x轴作垂线，两条垂线及C的准线和x轴围成边长为4的正方形，点M在第一象限.
（1）求抛物线C的方程及点M的坐标；
（2）过点M作倾斜角互补的两条直线分别与抛物线C交于A，B两点，且直线AB过点（0，-1），求
的面积.
已知函数
，
.
（1）当
时，证明：
；
（2）若
，求k的取值范围.
如图，四边形ABCD内接于圆
，BD是圆的直径，
于点E，DA平分
.
（1）证明：AE是圆的切线；
（2）如果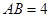
，
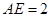，求CD.
已知曲线
的直角坐标方程为
. 以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系. P是曲线上一点，
，
，将点P绕点O逆时针旋转角
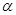后得到点Q，
，点M的轨迹是曲线
.
（1）求曲线的极坐标方程；
（2）求
的取值范围.
设不等式
的解集为M，
.
（1）证明：
；
（2）比较
与
的大小，并说明理由.