已知集合 ,
, ,则
,则 .
.
已知数列 是公差为2的等差数列,
是公差为2的等差数列,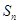 是
是 的前n项和,则
的前n项和,则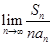 = .
= .
函数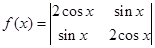 的最小正周期为 .
的最小正周期为 .
某小组中有6名女同学和4名男同学,从中任意挑选3名同学组成环保志愿者宣传队,则这个宣传队由2名女同学和1名男同学组成的概率是 (结果用分数表示).
圆柱M的底面直径与高均等于球O的直径,则圆柱M与球O的体积之比 .
.
已知 、
、 是平面上两个不共线的单位向量,向量
是平面上两个不共线的单位向量,向量 ,
, .若
.若 ,则实数
,则实数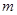 = .
= .
二项式 的展开式中含
的展开式中含 一次幂的项是第 项.
一次幂的项是第 项.
已知直线 ,
, ,若直线
,若直线 与
与 的夹角为
的夹角为 ,则
,则 = .
= .
设变量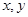 满足约束条件
满足约束条件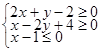 ,则目标函数
,则目标函数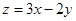 的最小值为 .
的最小值为 .
阅读右边的程序框图,如果输出的函数值 在区间
在区间 内,则输入的实数
内,则输入的实数 的取值范围是
的取值范围是 .
.
若等差数列 的首项为
的首项为 公差为
公差为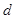 ,前
,前 项的和为
项的和为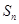 ,则数列
,则数列 为等差数列,且通项为
为等差数列,且通项为 .类似地,请完成下列命题:若各项均为正数的等比数列
.类似地,请完成下列命题:若各项均为正数的等比数列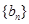 的首项为
的首项为 ,公比为
,公比为 ,前
,前 项的积为
项的积为 ,则 .
,则 .
若集合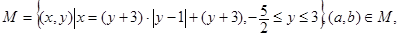 且对
且对 中其它元素
中其它元素 ,总有
,总有 则
则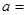 .
.
已知 ,
, ,
,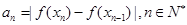 ,
, ,则
,则 的最大值等于 .
的最大值等于 .
平面直角坐标系中,如果 与
与 都是整数,就称点
都是整数,就称点 为整点,命题:
为整点,命题:
①存在这样的直线,既不与坐标轴平行又不经过任何整点;
②如果 与
与 都是无理数,则直线
都是无理数,则直线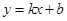 不经过任何整点;
不经过任何整点;
③如果 与
与 都是有理数,则直线
都是有理数,则直线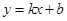 必经过无穷多个整点;
必经过无穷多个整点;
④存在恰经过一个整点的直线;其中的真命题是 (写出所有真命题编号).
某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )

已知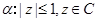 ,
, .若
.若 是
是 的充分非必要条件,则实数
的充分非必要条件,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
若 ,则称点
,则称点 在抛物线C:
在抛物线C: 外.已知点
外.已知点 在抛物线C:
在抛物线C: 外,则直线
外,则直线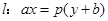 与抛物线C的位置关系是( )
与抛物线C的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.不能确定 |
在过正方体AC1的8个顶点中的3个顶点的平面中,能与三条棱CD 、A1D1、 BB1所成的角均相等的平面共有( )
A.1 个 B.4 个 C.8 个 D.12个
如图,直三棱柱 的底面
的底面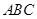 是等腰直角三角形,
是等腰直角三角形, ,侧棱
,侧棱 底面
底面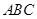 ,且
,且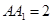 ,
,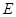 是
是 的中点.
的中点.
(1)求直三棱柱 的全面积;
的全面积;
(2)求异面直线 与
与 所成角
所成角 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);
已知函数
 .
.
(1)讨论函数 的奇偶性;
的奇偶性;
(2)若函数 在
在 上为减函数,求
上为减函数,求 的取值范围.
的取值范围.
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”, 并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
(1)试估算该市“足球迷”的人数,并指出其中“铁杆足球迷”约为多少人;
(2)该市要举办一场足球比赛,已知该市的足球场可容纳10万名观众.根据调查,如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看.如果票价提高 元/张
元/张 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
已知点 是椭圆
是椭圆 上任一点,点
上任一点,点 到直线
到直线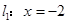 的距离为
的距离为 ,到点
,到点 的距离为
的距离为 ,且
,且 .直线
.直线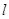 与椭圆
与椭圆 交于不同两点
交于不同两点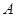 、
、 (
(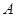 ,
, 都在
都在 轴上方) ,且
轴上方) ,且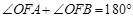 .
.
(1)求椭圆 的方程;
的方程;
(2)当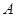 为椭圆与
为椭圆与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线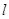 方程;
方程;
(3)对于动直线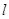 ,是否存在一个定点,无论
,是否存在一个定点,无论 如何变化,直线
如何变化,直线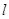 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
若数列 满足条件:存在正整数
满足条件:存在正整数 ,使得
,使得 对一切
对一切 都成立,则称数列
都成立,则称数列 为
为 级等差数列.
级等差数列.
(1)已知数列 为2级等差数列,且前四项分别为
为2级等差数列,且前四项分别为 ,求
,求 的值;
的值;
(2)若 为常数),且
为常数),且 是
是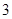 级等差数列,求
级等差数列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值时数列
取最小正值时数列 的前3
的前3 项和
项和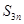 ;
;
(3)若 既是
既是 级等差数列
级等差数列 ,也是
,也是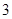 级等差数列,证明:
级等差数列,证明: 是等差数列.
是等差数列.