设复数
(其中
为虚数单位)，则
的虚部为（ ）
A． |
B．4 | C． |
D． |
的最大值为（ ）
| A．0 | B． |
C． |
D． |
下列有关命题的说法正确的是（ ）
A．命题“若 ”的否命题为：“若 ”； |
B．“ ”是“ ”的必要不充分条件； |
C．命题“  ,使得 ”的否定是：“  ,均有 ”； |
D．命题“若 ”的逆否命题为真命题. |
已知
，
，则
（ ）
A． |
B． |
C． 或 |
D． |
已知向量
,
且
，则
的最小值为（ ）
A． |
B．6 | C．12 | D． |
若双曲线
：
与抛物线
的准线交于
两点，且
，则
的值是（ ）
| A．1 | B． |
C．4 | D．13 |
如果在一次试验中，测得(
)的四组数值分别是
 |
1 |
2 |
3 |
4 |
 |
3 |
3.8 |
5.2 |
6 |
根据上表可得回归方程
，据此模型预报当为5时，的值为（ ）
A．6.9 B．7.1 C．7.04 D．7.2
已知函数
是R上的奇函数，且当
时，
，设函数 
,若
，则实数
的取值范围是（ ）
A． |
B． |
| C．(1,2) | D． |
已知空间几何体的三视图如图所示，则该几何体的体积是（ ）
A． |
B． |
C．4 | D． |
已知函数
，集合
，
，记
分别为集合
中的元素个数，那么下列结论不正确的是（ ）
A． |
B． |
C． |
D． |
执行如图所示程序框图，若输入
的值为2，则输出的
.
如图，目标函数
的可行域为四边形
(含边界)，若点
是该目标函数取最小值时的最优解，则
的取值范围是 .
在圆
内，过点
的最长弦与最短弦分别为
与
,则四边形
的面积为 .
一艘海轮从
处出发，以每小时20海里的速度沿南偏东40°方向直线航行．30分钟后到达
处．在
处有一座灯塔，海轮在处观察灯塔，其方向是南偏东70°，在处观察灯塔，其方向是北偏东65°，那么、两点间的距离是 .
已知函数
的定义域［-1，5］，部分对应值如表，的导函数
的图象如图所示，下列关于函数的命题:
①函数的值域为
；
②函数在
上是减函数；
③当
时，函数
最多有4个零点；
④如果当
时，的最大值是2，那么
的最大值为4.
其中正确命题的序号是(写出所有正确命题的序号) .
某数学兴趣小组有男女生各
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位：分).已知男生数据的中位数为
，女生数据的平均数为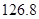
.
（1）求
，
的值；
（2）现从成绩高于分的同学中随机抽取两名同学，求抽取的两名同学恰好为一男一女的概率.
设函数
（
），其图象的两个相邻对称中心的距离为
.
（1）求函数
的解析式；
（2）若△
的内角为
所对的边分别为
（其中
），且
，
,
面积为
，求
的值.
如图，四边形PCBM是直角梯形，
，
，
，
．又
，
，
，直线
与直线
所成的角为60°．
（1）求证：
；
（2）求三棱锥
的体积.
在数列
中，已知
,
,
.
（1）求数列的通项公式；
（2）设数列
，求
的前
项和
.
已知向量
，
，且
．
(1)求点
的轨迹
的方程；
(2)设曲线与直线
相交于不同的两点
，又点
，当
时，求实数
的取值范围．
已知
).
（1）若
时，求函数
在点
处的切线方程；
（2）若函数
在
上是减函数，求实数
的取值范围；
（3）令
是否存在实数，当
是自然对数的底）时，函数
的最小值是
.若存在，求出的值；若不存在，说明理由.