已知 ,
, ,且向量
,且向量 和
和 垂直,则
垂直,则

 的值为( )
的值为( )
| A.0 | B.1 | C. |
D. |
在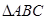 中,
中,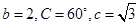 ,则角
,则角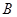 的大小为( )
的大小为( )
A.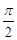 |
B.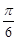 |
C.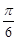 或 或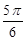 |
D.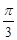 |
在 中,
中, c,
c, b.若点
b.若点 满足
满足 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
等差数列 中,
中, 公差
公差 ,那么使
,那么使 的前
的前 项和
项和 最大的
最大的 值为( )
值为( )
A. |
B. |
C. 或 或 |
D. 或 或 |
△ABC中,| |=5,|
|=5,| |=8,
|=8, ·
· =20,则|
=20,则| |为( )
|为( )
A. |
B. |
C. |
D. |
△ABC 中,若a、b、c成等比数例,且c = 2a,则cos B等于 ( )
A. |
B. |
C. |
D. |
已知数列 满足:
满足: ,
, ,
, ,那么使
,那么使 成立的
成立的 的最大值为( )
的最大值为( )
| A.4 | B.5 | C.24 | D.25 |
 中,
中, 是线段
是线段 的中点且
的中点且 是线段
是线段 上一个动点,若
上一个动点,若 ,则
,则 的最小值为( )
的最小值为( )
A. |
B. |
C. |
D. |
已知 ,把数列
,把数列 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,
记A(m,n)表示第m行的第n个数,则A(10,12)=( )
A. |
B. |
C. |
D. |
已知 为
为 所在平面内一点,满足
所在平面内一点,满足 ,则点
,则点 是
是 的( )
的( )
| A.外心 | B.内心 | C.垂心 | D.重心 |
已知等比数列{ }是递增数列,
}是递增数列, 是{
是{ }的前
}的前 项和.若
项和.若 ,
, 是方程
是方程 的两个根,则
的两个根,则 =________.
=________.
已知向量 ,
, ,则
,则 在
在 方向上的投影等于
方向上的投影等于
已知向量 、
、 满足:
满足: ,
, ,
, ,则
,则 ________
________
已知等差数列 的公差
的公差 ,且
,且 成等比数列,则
成等比数列,则 的值是_______.
的值是_______.
已知a=(2,-1), b=( ,3).若a与b的夹角为钝角,则
,3).若a与b的夹角为钝角,则 的取值范围是
的取值范围是
对于正项数列 ,定义Hn=
,定义Hn= 为
为 的“光阴”值,现知某数列的“光阴”值为
的“光阴”值,现知某数列的“光阴”值为 ,则数列
,则数列 的通项公式为________.
的通项公式为________.
已知 ,且实数
,且实数 ,则
,则 与
与 的夹角取值范围 .
的夹角取值范围 .
已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量 ,
, ,
, .
.
(1)若 //
// ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2)若 ⊥
⊥ ,边长
,边长 ,角
,角
 ,求ΔABC的面积 .
,求ΔABC的面积 .
已知等差数列{ }中,
}中, ,前
,前 项和
项和 .
.
(1)求通项 ;
;
(2)若从数列{ }中依次取第
}中依次取第 项、第
项、第 项、第
项、第 项…第
项…第 项……按原来的顺序组成一个新的数列{
项……按原来的顺序组成一个新的数列{ },求数列{
},求数列{ }的前
}的前 项和
项和 .
.
已知 、
、 、
、 分别为
分别为 的三边
的三边 、
、 、
、 所对的角,向量
所对的角,向量 ,
, ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, ,
, 成等差数列,且
成等差数列,且 ,求边
,求边 的长.
的长.
已知数列 ,
,  满足条件:
满足条件:
 ,
,  .
.
(1)求证数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ,并求使得
,并求使得 对任意
对任意 N*都成立的正整数
N*都成立的正整数 的最小值.
的最小值.
已知数列{ }的前
}的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)求证:{ }是等差数列;
}是等差数列;
(2)求 表达式;
表达式;
(3)若 ,求证:
,求证: .
.