设集合,则
设则
若向量满足:,则()
有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()
| A. |
60种
|
B. |
70种
|
C. |
75种
|
D. |
150种
|
已知椭圆的左、右焦点为,离心率为,过的直线交于两点,若的周长为,则的方程为
曲线
在点
处切线的斜率等于
正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
| A. |
|
B. |
|
C. |
|
D. |
|
已知双曲线的离心率为2,焦点为、,点在上,若,则 ( )
等比数列
中,
,则数列
的前8项和等于
6
5
4
3
已知二面角为,,,为垂足,,则异面直线与所成角的余弦值为()
函数
的图象与函数
的图象关于直线
对称,则
的反函数是
设
满足约束条件
,则
的最大值为.
直线和是圆的两条切线,若与的交点为,则与的夹角的正切值等于 .
若函数
在区间
是减函数,则
的取值范围是.
的内角的对边分别为,已知,,求.
等差数列的前项和为,已知为整数,且.
(1)求的通项公式;
(2)设,求数列的前项和.
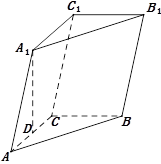
如图,三棱柱中,点在平面内的射影在上,,.
(1)证明:;
(2)设直线与平面的距离为,求二面角的大小.
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为各人是否需使用设备相互独立.
(1)求同一工作日至少3人需使用设备的概率;
(2)表示同一工作日需使用设备的人数,求的数学期望.
已知抛物线的焦点为,直线与轴的交点为,与的交点为,且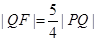 .
.
(1)求的方程;
(2)过的直线与相交于两点,若的垂直平分线与相较于两点,且四点在同一圆上,求的方程.
函数
.
(1)讨论
的单调性;
(2)设
,证明:
.

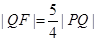 .
.