全国普通高等学校招生统一考试理科数学-优题课

已知集合 $M = \{- 1, 0, 1\}$ ， $N = \{0, 1, 2\}$ ，则 $M \cup N =$

\{- 1, 0, 1\}

\{- 1, 0, 1, 2\}

\{- 1, 0, 2\}

\{0, 1\}

已知复数 $z$ 满足 $(3 + 4 i) z = 25$ ，则 $z =$ （）

A．

3 - 4 i

B．

3 + 4 i

C．

- 3 - 4 i

D．

- 3 + 4 i

若变量 $x$ 、 $y$ 满足约束条件 $\{\begin{cases} \begin{matrix} y \leq x \\ x + y \leq 1 \\ y \leq - 1 \end{matrix} \end{cases},$ ，且 $z = 2 x + y$ 的最大值和最小值分别为 $M$ 和 $m$ ，则 $M - m =$ （）

A．

B．

C．

D．

若实数 $k$ 满足 $0 < k < 9$ ，则曲线 $\frac{x^{2}}{25} - \frac{y^{2}}{9 - k} = 1$ 与曲线 $\frac{x^{2}}{25 - k} - \frac{y^{2}}{9} = 1$ 的（）

A．

离心率相等

B．

虚半轴长相等

C．

实半轴长相等

D．

焦距相等

已知向量 $\underset{a}{\to} = (1, 0, - 1)$ ，则下列向量中与 $\underset{a}{\to}$ 成 $60^{°}$ 的是（）

A．

(- 1, 1, 0)

B．

(1, - 1, 0)

C．

(0, - 1, 1)

D．

(- 1, 0, 1)

已知某地区中小学生人数和近视情况分别如图1和如图2所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2℅的学生进行调查，则样本容量和抽取的高中生近视人数分别为（）

A．

200，20

B．

100，20

C．

200，10

D．

100，10

若空间中四条直线两两不同的直线 $l_{1}$ 、 $l_{2}$ 、 $l_{3}$ 、 $l_{4}$ ，满足 $l_{1} ⊥ l_{2}$ ， $l_{2} / / l_{3}$ ， $l_{3} ⊥ l_{4}$ ，则下列结论一定正确的是（）

A．	$l_{1} ⊥ l_{4}$	B．	$l_{1} / / l_{4}$
C．	$l_{1}$ 、 $l_{4}$ 既不平行也不垂直	D．	$l_{1}$ 、 $l_{4}$ 的位置关系不确定

设集合 $A = \{(x_{1}, x_{^{2}}, x_{3}, x_{4}, x_{5}) | x_{1} \in \{- 1, 0, 1\}, i = 1, 2, 3, 4, 5\}$ ，那么集合 $A$ 中满足条件" $1 \leq |x_{1}| + |x_{2}| + |x_{3}| + |x_{4}| + |x_{5}| \leq 3$ "的元素个数为

不等式 $|x - 1| + |x + 2| \geq 5$ 的解集为.

曲线 $y = e^{- 5 x} + 2$ 在点 $(0, 3)$ 处的切线方程为.

在 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 所对应的边分别为 $a$ 、 $b$ 、 $c$ ，已知 $b \cos C + c \cos B = 2 b$ ，则 $\frac{a}{b} =$ .

若等比数列 $\{a_{n}\}$ 的各项均为正数，且 $a_{10} a_{11} + a_{9} a_{12} = 2 e^{5}$ ，则 $\ln a_{1} + \ln a_{2} + . . . . . . + \ln a_{20} =$ .

如图,在平行四边形 $A B C D$ 中,点 $E$ 在 $A B$ 上且 $E B = 2 A E, A C$ 与 $D E$ 交于点 $F$ ,则 $\frac{S_{∆ C D F}}{S_{∆ A E F}} =$ .

已知函数 $f (x) = A \sin (x + \frac{π}{4})$ ， $x \in R$ ，且 $f (\frac{5}{12} π) = \frac{3}{2}$ .
（1）求 $A$ 的值；
（2）若 $f (θ) + f (- θ) = \frac{3}{2}$ ， $θ \in (0, \frac{π}{2})$ ，求 $f (\frac{3}{4} π - θ)$ .

随机观测生产某种零件的某工厂名工人的日加工零件数（单位：件），获得数据如下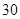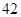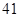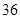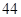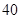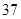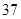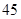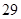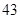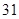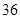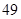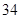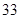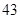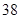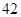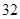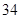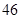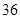：、、、、、、、、、、、、、、、、、、、、、、、、，根据上述数据得到样本的频率分布表如下：

分组	频数	频率



		$f_{1}$
		$f_{2}$

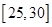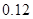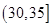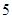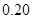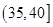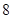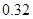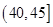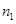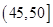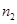（1）确定样本频率分布表中 $n_{1}, n_{2}, f_{1} 和 f_{2}$ 的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）根据样本频率分布直方图，求在该厂任取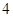人，至少有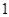人的日加工零件数落在区间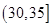的概率.

如图，四边形 $A B C D$ 为正方形， $P D ⊥ A B C$ 平面 $A B C D$ ， $∠ D P C = 30^{°}$ ， $A F ⊥ P C$ 于点 $F$ ， $F E ∥ C D$ ，交 $P D$ 于点 $E$ .

（1）证明： $C F ⊥$ 平面 $A D F$ ；
（2）求二面角 $D - A F - E$ 的余弦值.

设数列 $\{a_{n}\}$ 的前 $n$ 项和为 $S_{n}$ ，满足 $S_{n} = 2 n a_{n - 1} - 3 n^{2} - 4 n$ ， $n \in N^{+}$ ，且 $S_{3} = 15$ .
（1）求 $a_{1}$ 、 $a_{2}$ 、 $a_{3}$ 的值；
（2）求数列 $\{a_{n}\}$ 的通项公式.

已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的一个焦点为 $(\sqrt{5}, 0)$ ，离心率为 $\frac{\sqrt{5}}{3}$ .
（1）求椭圆 $C$ 的标准方程；
（2）若动点 $P (x_{0}, y_{0})$ 为椭圆外一点，且点 $P$ 到椭圆 $C$ 的两条切线相互垂直，求点 $P$ 的轨迹方程.

设函数 $f (x) = \frac{1}{\sqrt{(x^{2} + 2 x + k)^{2} + 2 (x^{2} + 2 x + k) - 3}}$ ，其中 $k < - 2$ .
（1）求函数 $f (x)$ 的定义域 $D$ （用区间表示）；
（2）讨论函数 $f (x)$ 在 $D$ 上的单调性；
（3）若 $k < - 6$ ，求 $D$ 上满足条件 $f (x) > f (1)$ 的 $x$ 的集合（用区间表示）.