下列手机软件图标中,属于中心对称的是()
下列运算正确的是()
A. |
B. |
C. |
D. |
要调查下列问题,你认为哪些适合抽样调查()
①市场上某种食品的某种添加剂的含量是否符合国家标准;
②检测某地区空气的质量;
③调查全市中学生一天的学习时间.
| A.①② | B.①③ | C.②③ | D.①②③ |
如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
| A.18 cm | B.22 cm | C.24 cm | D.26 cm |

某校篮球课外活动小组21名同学的身高如下表
| 身高(cm) |
170 |
176 |
178 |
182 |
184 |
| 人数 |
4 |
6 |
5 |
4 |
2 |
则该篮球课外活动小组21名同学身高的众数和中位数分别是()
A.176,176 B.176,177 C.176,178 D.184,178
半径为2的圆中,弦AB、AC的长分别2和2 ,则∠BAC的度数是()
,则∠BAC的度数是()
A.15° B.105° C.15°或75° D.15°或105°
一个口袋轴装有3个红球,4个绿球,2个黄球,每个球除颜色外其它都相同,搅匀后随机地从中摸出一个球不是红球的概率是()
A. |
B. |
C. |
D. |
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是()
A.矩形 B.菱形 C.正方形 D.梯形
某种商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为()
| A.200元 | B.240元 | C.250元 | D.300元 |
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则函数y= 与y=bx+c在同一直角坐标系内的大致图象是()
与y=bx+c在同一直角坐标系内的大致图象是()
函数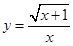 的自变量
的自变量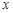 的取值范围是 .
的取值范围是 .
若 是同一个数的平方根,则x的值为 .
是同一个数的平方根,则x的值为 .
三角形的三条边长分别是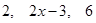 ,则
,则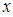 的取值范围是 .
的取值范围是 .
2014年3月8日马航失踪后,党中央、国务院高度重视,3月12日前,我国已划定长90海里,宽25海里,总面积约2250平方海里(约合7717平方公里)的长方形区域为的海上搜救范围,1平方公里=1×106平方米,对7717平方公里用科学计数法表示为__________ 平方米。
计算:tan245°-2sin30°+( ﹣1)0 -
﹣1)0 - =
=
如果一组数据 -2,0,3,5,x的极差是9,那么这组数据的平均数是 ____.
如图,网格图中每个小正方形的边长为 ,则弧AB的弧长
,则弧AB的弧长 .
.
如图,是一组按照某种规律摆放而成的图案,则图6中三角形的个数是 .
先化简,再求代数式 的值,其中
的值,其中
△ABC在平面直角坐标系xOy中的位置如所示.
(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移3个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
根据以上图表提供的信息,解答下列问题:
(1)写出表中x, y的数值;
(2)请补全频数分布直方图;
(3)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(4)获奖成绩的中位数落在哪个分数段?
如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P= ,求AC的长.
,求AC的长.
我区某房地产开发公司于2013年5月份完工一商品房小区,6月初开始销售,其中6月的销售单价为0.7万元/m2,7月的销售单价为0.72万元/m2,且每月销售价格 (单位:
(单位: )与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为
)与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为 (单位:
(单位: ),其中y2=-2000x+26000(6≤x≤11,x为整数).
),其中y2=-2000x+26000(6≤x≤11,x为整数).
(1)求 与月份
与月份 的函数关系式;
的函数关系式;
(2)6~11月中,哪一个月的销售额最高?最高销售额为多少万元?
(3)2013年11月时,因受某些因素影响,该公司销售部预计12月份的销售面积会在11月销售面积基础上减少 ,于是决定将12月份的销售价格在11月的基础上增加
,于是决定将12月份的销售价格在11月的基础上增加 ,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为
,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为 万元,请根据以上条件求出
万元,请根据以上条件求出 的值为多少?
的值为多少?
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,∴∠FDG=180°,点F、D、G共线。
根据__ __________,易证△AFG≌_ _______,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系_ ___时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。
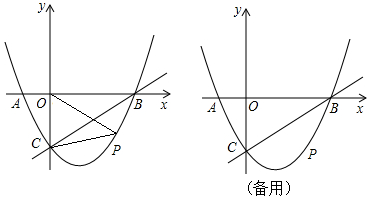
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.