复数 ,则它的共轭复数
,则它的共轭复数 在复平面内对应的点位于( )
在复平面内对应的点位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
推理:因为平行四边形对边平行且相等,而矩形是特殊的平行四边形,所以矩形的对边平行且相等.以上推理的方法是( )
| A.合情推理 | B.演绎推理 | C.归纳推理 | D.类比推理 |
在区间 内不是增函数的是( )
内不是增函数的是( )
A. |
B. |
C. |
D. |
函数 的图象上一点
的图象上一点 处的切线的斜率为( )
处的切线的斜率为( )
A.- |
B. |
C.- |
D.- |
用反证法证明命题“三角形的内角至多有一个钝角”时,假设的内容应为( )
| A.假设至少有一个钝角 | B.假设至少有两个钝角 |
| C.假设没有一个钝角 | D.假设没有一个钝角或至少有两个钝角 |
 等于( )
等于( )
A. |
B.2 | C. |
D. |
已知复数 且
且 ,则
,则 的最小值是( )
的最小值是( )
A. |
B. |
C. |
D. |
函数 的部分图像如图所示,则
的部分图像如图所示,则 的解析式可以是( )
的解析式可以是( )
A. |
B. |
C. |
D. |
六个面都是平行四边形的四棱柱称为平行六面体。如,在平行四边形 中,有
中,有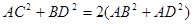 ,那么在图(2)的平行六面体
,那么在图(2)的平行六面体 中有
中有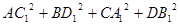 等于( )
等于( )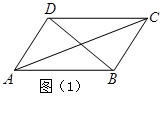
A. |
B. |
C.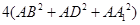 |
D. |
对于三次函数 ,定义
,定义 是
是 的导函数
的导函数 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数 都关于点
都关于点 对称:
对称:
②存在三次函数 ,若
,若 有实数解
有实数解 ,则点
,则点 为函数
为函数 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则:
,则: 
其中所有正确结论的序号是( ).
| A.①②④ | B.①②③ | C.①③④ | D.②③④ |
已知 是虚数单位,则
是虚数单位,则 =_____________.
=_____________.
由直线 ,曲线
,曲线 及
及 轴所围图形的面积为
轴所围图形的面积为
已知函数 有极大值和极小值,则实数
有极大值和极小值,则实数 的取值范围是
的取值范围是
若 上是减函数,则
上是减函数,则 的最大值是
的最大值是
设 表示不超过
表示不超过 的最大整数,如
的最大整数,如 .我们发现:
.我们发现: ;
; ;
; ;
;
.......
通过合情推理,写出一般性的结论 (用含 的式子表示)
的式子表示)
设函数
 ,已知曲线
,已知曲线 在点
在点 处的切线方程是
处的切线方程是 .
.
(1)求 的值;并求出函数的单调区间;
的值;并求出函数的单调区间;
(2)求函数 在区间
在区间 上的最值.
上的最值.
设数列 满足
满足 .
.
(1)求 ;
;
(2)由(1)猜想 的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分)
的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分)
已知 ,证明:
,证明: ,并利用上述结论求
,并利用上述结论求 的最小值(其中
的最小值(其中 .
.
已知函数 ,
, ,
, 为自然对数的底数.
为自然对数的底数.
(I)求函数 的极值;
的极值;
(2)若方程 有两个不同的实数根,试求实数
有两个不同的实数根,试求实数 的取值范围;
的取值范围;
甲、乙两个工厂,甲厂位于一直线河岸的岸边 处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的
处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的 处,乙厂到河岸的垂足
处,乙厂到河岸的垂足 与
与 相距50千米,两厂要在此岸边
相距50千米,两厂要在此岸边 之间合建一个供水站
之间合建一个供水站 ,从供水站到甲厂和乙厂的水管费用分别为每千米3
,从供水站到甲厂和乙厂的水管费用分别为每千米3 元和5
元和5 元,若
元,若 千米,设总的水管费用为
千米,设总的水管费用为 元,如图所示,
元,如图所示,
(1)写出 关于
关于 的函数表达式;
的函数表达式;
(2)问供水站 建在岸边何处才能使水管费用最省?
建在岸边何处才能使水管费用最省? 
已知函数 (
( )
)
(1)讨论函数 的单调性;
的单调性;
(2)若函数 在
在 处取得极值,不等式
处取得极值,不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 时,证明不等式
时,证明不等式  .
.