某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中不低于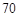 分的学生数是 .
分的学生数是 .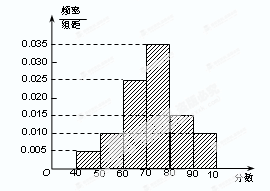
在数列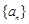 中,
中,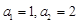 ,且
,且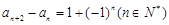 ,则
,则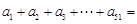 .
.
在 中,
中, ,则
,则 的大小为 .
的大小为 .
已知等比数列{an}中,a1+a2=9,a1a2a3=27,则{an}的前n项和  。
。
函数 的最小正周期为 。
的最小正周期为 。
某单位有200名职工,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是
设变量 、
、 满足约束条件
满足约束条件 ,则z=2x+3y的最大值为
,则z=2x+3y的最大值为
在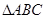 中,角
中,角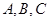 的对边分别是
的对边分别是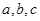 ,若
,若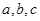 成等差数列,
成等差数列,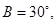
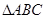 的面积为
的面积为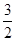 ,则
,则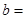 ____.
____.
一组数据6,7,7,8,7的方差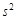 = .
= .
袋中有1个白球,2个黄球,先从中摸出一球,再从剩下
的球中摸出一球,两次都是黄球的概率为 .
执行右面的流程图,输出的S = .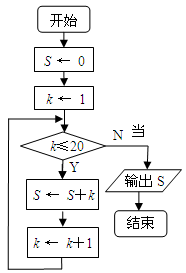
已知x<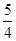 ,则函数y=4x-2+
,则函数y=4x-2+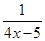 的最大值是 .
的最大值是 .
已知点E在正△ABC的边AB上,AE = 2EB,在边AC上任意取一点P,则“△AEP的面积恰好小于△ABC面积的一半”的概率为 .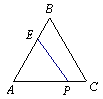
公差不为零的等差数列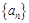 中,
中,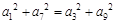 ,记
,记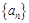 的前
的前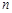 项和为
项和为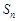 ,其中
,其中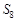
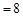 ,则
,则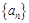 的通项公式为
的通项公式为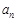 = .
= .
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题: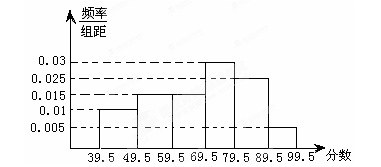
(1)79.5~89.5这一组的频率、频数分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格)和平均分.
设数列{an}是一个公差为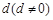 的等差数列,已知它的前10项和为
的等差数列,已知它的前10项和为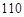 ,且a1,a2,a4 成等比数列.
,且a1,a2,a4 成等比数列.
(1)求数列{an}的通项公式;
(2)若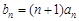 ,求数列
,求数列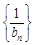 的前
的前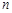 项和Tn .
项和Tn .
在△ABC中,角A,B,C的对边分别为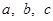 ,且A,B,C成等差数列。
,且A,B,C成等差数列。
(1)若 ,
,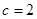 ,求△ABC的面积;
,求△ABC的面积;
(2)若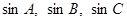 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。
已知: ,当
,当 时,
时, ;
;
当 时,
时, 。
。
(1)求 的解析式
的解析式
(2)解x的不等式
某厂生产A产品的年固定成本为250万元,若A产品的年产量为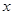 万件,则需另投入成本
万件,则需另投入成本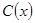 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时,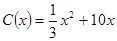 ;A产品年产量大于80万件时,
;A产品年产量大于80万件时,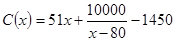 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
(1)写出L关于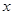 的函数解析式
的函数解析式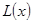 ;
;
(2)当年产量为多少时,该厂生产A产品所获的利润最大?
已知数列{an }的前n项和为Sn,满足an ¹ 0,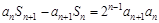 ,
,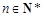 .
.
(1)求证: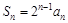 ;
;
(2)设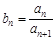 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.