若幂函数的解析式为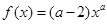 ,则
,则
 的值为 ________.
的值为 ________.
若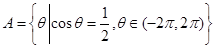 ,则集合
,则集合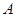 的子集有______个.
的子集有______个.
已知函数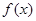 的图象是连续不断的,观察下表:
的图象是连续不断的,观察下表:
| x |
-2 |
-1 |
0 |
1 |
2 |
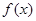 |
-6 |
3 |
-3 |
-2 |
1 |
函数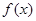 在区间[-2,2]上的零点至少有_____个.
在区间[-2,2]上的零点至少有_____个.
若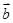 与
与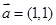 垂直,且
垂直,且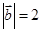 ,则
,则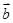 的坐标为_______.
的坐标为_______.
三个数 的大小关系为____________ .(按从小到大的顺序填写)
的大小关系为____________ .(按从小到大的顺序填写)
已知函数 的图象不经过第三象限,则实数
的图象不经过第三象限,则实数 的取值范围是____________.
的取值范围是____________.
已知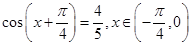 ,则
,则
设 ,则
,则
若函数f(x)同时具有以下两个性质:①f(x)是偶函数;②对任意实数x,都有f(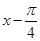 )= f(
)= f(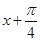 ),则下列函数中,符合上述条件的有_________.(填序号)
),则下列函数中,符合上述条件的有_________.(填序号)
①f(x)=cos4x ②f(x)=sin(2x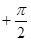 ) ③f(x)=sin(4x
) ③f(x)=sin(4x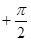 ) ④f(x) = cos(
) ④f(x) = cos(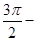 4x)
4x)
已知偶函数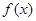 满足:
满足: ,且当
,且当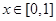 时,
时,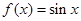 ,其图象与直线
,其图象与直线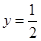 在
在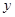 轴右侧的交点按横坐标从小到大依次记为
轴右侧的交点按横坐标从小到大依次记为 ,则
,则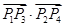 等于 .
等于 .
已知函数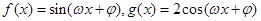 若对任意的
若对任意的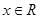 都有
都有 ,则
,则 =__________.
=__________.
定义运算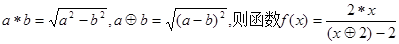 的奇偶性为 .
的奇偶性为 .
已知函数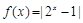 ,当
,当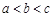 时,有
时,有 .给出以下结论:
.给出以下结论:
(1)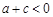 ;(2)
;(2)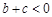 ;(3)
;(3)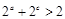 ;(4)
;(4)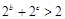 .
.
其中正确的结论序号为_________
如图,在平面直角坐标系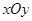 中,以
中,以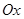 轴为始边作两个锐角
轴为始边作两个锐角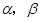 ,它们的终边分别交单位圆于
,它们的终边分别交单位圆于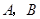 两点.已知
两点.已知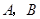 两点的横坐标分别是
两点的横坐标分别是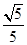 ,
,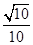 .
.
(1)求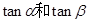 的值;
的值;
(2)求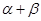 的值.
的值.
已知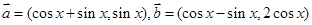 ,设
,设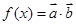 .
.
(1)求函数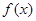 的最小正周期,并写出
的最小正周期,并写出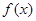 的减区间;
的减区间;
(2)当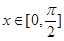 时,求函数
时,求函数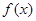 的最大值及最小值.
的最大值及最小值.
已知函数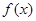 的定义域是
的定义域是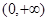 ,且满足
,且满足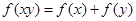 ,
,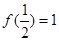 ,
,
如果对于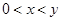 ,都有
,都有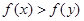 .
.
(1)求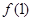 ;
;
(2)解不等式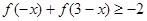 .
.
商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
已知坐标平面内O为坐标原点,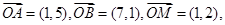 P是线段OM上一个动点.当
P是线段OM上一个动点.当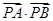 取最小值时,求
取最小值时,求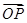 的坐标,并求
的坐标,并求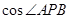 的值.
的值.
设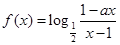 为奇函数,
为奇函数,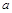 为常数.
为常数.
(1)求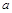 的值;
的值;
(2)证明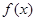 在区间(1,+∞)内单调递增;
在区间(1,+∞)内单调递增;
(3)若对于区间[3,4]上的每一个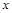 的值,不等式
的值,不等式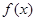 >
>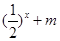 恒成立,求实数
恒成立,求实数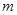 的取值范围.
的取值范围.