若集合 ,
, 则集合
则集合 _______.
_______.
已知向量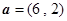 ,b=(-2,4),则a+b= _______.
,b=(-2,4),则a+b= _______.
sin660 的值是_______.
的值是_______.
已知角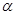 的终边过点
的终边过点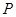 (-5,12),则
(-5,12),则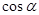 =________.
=________.
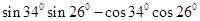 的值为_____.
的值为_____.
已知数列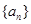 为等差数列,且
为等差数列,且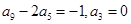 ,则公差
,则公差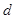 = .
= .
数列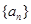 的通项公式
的通项公式 ,它的前n项和为
,它的前n项和为 ,则
,则 _________.
_________.
已知数列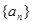 是等差数列,且
是等差数列,且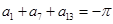 ,则
,则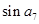 = .
= .
△ABC的内角A、B、C的对边分别为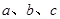 ,若
,若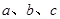 成等比数列,且
成等比数列,且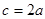 ,则
,则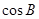 = .
= .
数列 中,
中, ,则通项
,则通项 ___________.
___________.
若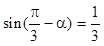 ,则
,则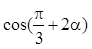 =______.
=______.
在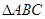 中,已知
中,已知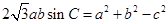 ,则
,则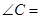 .
.
已知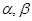
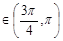 ,sin(
,sin(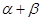 )=-
)=-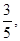
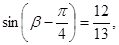 则
则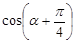 等于 .
等于 .
设动直线 与函数
与函数 和
和 的图象分别交于
的图象分别交于 、
、 两点,则
两点,则 的最大值为____.
的最大值为____.
已知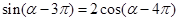 ;求
;求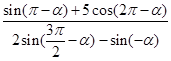 的值.
的值.
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且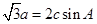 .
.
(1)确定角C的大小:
(2)若c=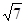 ,且△ABC的面积为
,且△ABC的面积为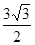
 ,求a+b的值.
,求a+b的值.
如图,以Ox为始边作角α与β(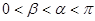 ) ,它们终边分别单位圆相交于点P、Q,已知点P的坐标为(
) ,它们终边分别单位圆相交于点P、Q,已知点P的坐标为( ,
,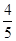 ).
).
(1)求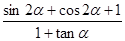 的值;
的值;
(2)若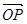 ·
· ,求
,求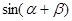 .
.
已知函数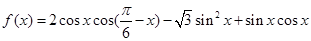 .
.
(1)求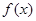 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)设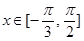 ,求
,求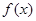 的值域.
的值域.
设等差数列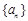 的前
的前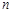 项和为
项和为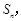 且
且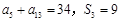 .
.
(1)求数列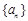 的通项公式及前
的通项公式及前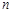 项和公式;
项和公式;
(2)设数列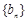 的通项公式为
的通项公式为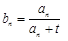 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得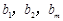
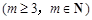 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
如图,在半径为 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在 上,设矩形
上,设矩形 的面积为
的面积为 .
.
(1)按下列要求写出函数关系式:
①设 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
②设 ,将
,将 表示成
表示成 的函数关系式.
的函数关系式.
(2)请你选用(1)中的一个函数关系式,求 的最大值.
的最大值.