已知向量
＝(5，－3)，
＝(－6，4)，则
＝( )
| A．(1，1) | B．(－1，－1) | C．(1，－1) | D．(－1，1) |
设全集
＝{1，2，3，4}，集合
＝{1，3}，
＝{4}，则
等于( )
| A．{2，4} | B．{4} | C．Φ | D．{1，3，4} |
已知命题
，则
为( )
A． |
B． |
C． |
D． |
计算
的结果是( )
A． |
B．2 | C． |
D．3 |
已知实数x，y满足
，则z＝4x＋y的最大值为( )
| A．10 | B．8 | C．2 | D．0 |
已知
是两条不同的直线，
是一个平面，则下列说法正确的是( )
A．若 ，则 |
B．若 ，则 |
C．若 ，则 |
D．若 ，则 |
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，一般情况下PM2.5的浓度越大，大气环境质量越差.右边的茎叶图表示的是成都市区甲乙两个监测站某10日内每天的PM2.5浓度读数(单位：
)，则下列说法正确的是( )
| A．这10日内甲、乙监测站读数的极差相等 |
| B．这10日内甲、乙监测站读数的中位数中，乙的较大 |
| C．这10日内乙监测站读数的众数与中位数相等 |
| D．这10日内甲、乙监测站读数的平均数相等 |
已知函数
(ω＞0)的图象与直线y＝－2的两个相邻公共点之间的距离等于π，则
的单调递减区间是( )
A． |
B． |
C． |
D． |
已知双曲线
(a＞0，b＞0)的一条渐近线与圆
相交于A，B两点，若|AB|=2，则该双曲线的离心率为( )
| A．8 | B．2 |
C．3 | D． |
已知定义在R上的函数f(x)的周期为4，且当x∈(－1，3]时，f(x)＝
，则函数
的零点个数是( )
| A．4 | B．5 | C．6 | D．7 |
已知
，
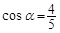，则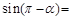
_____________.
如图是一个几何体的三视图，则该几何体的体积是____________
当
时，函数
的最小值是_______________.
运行如图所示的程序框图，则输出的运算结果是_____________
已知
(a＞0且a≠1)是定义在R上的单调递减函数，记a的所有可能取值构成集合A；P(x，y)是椭圆
上一动点，
与点P关于直线y＝x＋1对称，记
的所有可能取值构成集合B，若随机的从集合A，B中分别抽出一个元素
，则
的概率是___________
已知等差数列
的前n项和为
，且
(1)求数列的通项公式；
(2)设
，求数列
的前n项和Tn.
在△ABC中，角A，B，C所对的边分别为a，b，c，已知向量
，
，且
(1)求角B的大小；
(2)求函数
的值域.
某地区为了解高二学生作业量和玩电脑游戏的情况，对该地区内所有高二学生采用随机抽样的方法，得到一个容量为200的样本.统计数据如下：
(1)已知该地区共有高二学生42500名，根据该样本估计总体，其中喜欢电脑游戏并认为作业不多的人有多少名？
(2)在A，B，C，D，E，F六名学生中，仅有A，B两名学生认为作业多.如果从这六名学生中随机抽取两名，求至少有一名学生认为作业多的概率.
如图，已知
的直径AB＝3，点C为上异于A，B的一点，
平面ABC，且VC＝2，点M为线段VB的中点.
(1)求证：
平面VAC；
(2)若AC＝1，求直线AM与平面VAC所成角的大小.
已知椭圆Γ：
(a＞b＞0)经过D(2，0)，E(1，
)两点.
(1)求椭圆Γ的方程；
(2)若直线
与椭圆Γ交于不同两点A，B，点G是线段AB中点，点O是坐标原点，设射线OG交Γ于点Q，且
.
①证明：
②求△AOB的面积.
已知函数
，其中a，b∈R
(1)当a＝3，b＝－1时，求函数f(x)的最小值；
(2)若曲线y＝f(x)在点(e，f(e))处的切线方程为2x－3y－e＝0(e＝2.71828 为自然对数的底数)，求a，b的值；
(3)当a＞0，且a为常数时，若函数h(x)＝x[f(x)＋lnx]对任意的x1＞x2≥4，总有
成立，试用a表示出b的取值范围.