已知x与y之间的一组数据：
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程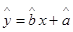
必过点( )
A.(1.5 ,4) B.(2,2) C.(1.5 ,0) D.(1,2)
如图，某几何体的正视图与侧视图都是边长为1的正方形且体积为
，则该几何体的俯视图可以是
如果
的展开式中各项系数之和为128，则展开式中
的系数是（ ）
| A．-2835 | B．2835 | C．21 | D．-21 |
已知
中，三个内角A，B，C的对边分别为a,b,c，若的面积为S，且
等于
A． |
B． |
C． |
D． |
点
到图形
上每一个点的距离的最小值称为点到图形的距离，那么平面内到定圆的距离与到定点
的距离相等的点的轨迹不可能是（ ）
| A．圆 | B．椭圆 | C．双曲线的一支 | D．直线 |
已知抛物线的顶点在原点，焦点在x轴的正半轴上，若抛物线的准线与双曲线5x2－y2= 20的两条渐近线围成的三角形的面积等于
，则抛物线的方程为
| A．y2=4x | B．y2=8x | C．x2=4y | D．x2=8y |
函数y＝2x－x2的图象大致是( )．
在下列区间中，函数f(x)＝ex＋4x－3的零点所在的区间( )
A．(－ ，0) |
B．(0，) |
C．(， ) |
D．(， ) |
若二项式(
)
展开式的常数项为20，则
的值为
A． |
B． |
C． |
D． |
已知
，则
A． |
B． |
C． |
D． |
某产品的广告费用
与销售额
的统计数据如下表：
| 广告费用（万元） |
3 |
4 |
5 |
6 |
| 销售额（万元） |
25 |
30 |
40 |
45 |
根据上表可得回归方程
中的
为7.据此模型预报广告费用为10万元时销售额为 （万元）.
已知实数
满足不等式组
那么目标函数
的最大值是 .
在样本的频率分布直方图中, 共有9个小长方 形, 若第一个长方形的面积为0.02, 前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160, 则中间一组（即第五组）的频数为 . 
设
，定义
为
的导数，即
，
，若
的内角
满足
，则
的值是 .
某种商品，现在定价p元，每月卖出n件，设定价上涨x成，每月卖出数量减少y成，每月售货总金额变成现在的z倍．
(1)用x和y表示z；
(2)设x与y满足y＝kx(0<k<1)，利用k表示当每月售货总金额最大时x的值；
(3)若y＝
x，求使每月售货总金额有所增加的x值的范围．
已知函数
（
为常数,
且
）的图象过点
.
（1）求实数的值;
（2）若函数
,试判断函数
的奇偶性,并说明理由
已知抛物线
的焦点为F2，点F1与F2关于坐标原点对称，直线m垂直于x轴（垂足为T），与抛物线交于不同的两点P,Q且
.
（I）求点T的横坐标
；
（II）若以F1,F2为焦点的椭圆C过点
.
①求椭圆C的标准方程；
②过点F2作直线l与椭圆C交于A,B两点，设
，若
的取值范围.