已知抛物线 的准线与双曲线
的准线与双曲线 交于A,B两点,点F为抛物线的焦点,若
交于A,B两点,点F为抛物线的焦点,若 为直角三角形,则双曲线的离心率是
为直角三角形,则双曲线的离心率是
A. |
B. |
C.2 | D.3 |
已知动点 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为 ,
, ,且
,且 ,则
,则 的最小值是( )
的最小值是( )
A. |
B. |
C. |
D. |
已知 ,那么
,那么 等于( )
等于( )
A. |
B. |
C. |
D. |
要得到函数 的导函数
的导函数 的图象,只需将
的图象,只需将 的图象( )
的图象( )
A.向左平移 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) |
B.向左平移 个单位,再把各点的纵坐标缩短到原来的 个单位,再把各点的纵坐标缩短到原来的 倍(横坐标不变) 倍(横坐标不变) |
C.向左平移 个单位,再把各点的纵坐标伸长到原来的 个单位,再把各点的纵坐标伸长到原来的 倍(横坐标不变) 倍(横坐标不变) |
D.向左平移 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) |
已知x,y满足条件 (k为常数),若目标函数
(k为常数),若目标函数 的最大值为8,则k=
的最大值为8,则k=
A. |
B. |
C. |
D.6 |
如图,设D是图中边长为4的正方形区域,E是D内函数 图象下方的点构成的区域(阴影部分).向D中随机投一点,则该点落入E中的概率为
图象下方的点构成的区域(阴影部分).向D中随机投一点,则该点落入E中的概率为
A. |
B. |
C. |
D. |

已知函数y=f(x)的周期为2,当x∈[-1,1]时f(x)=x2,那么函数y=f(x)的图象与函数y=|lg x|的图象的交点共有( )
| A.10个 | B.9个 | C.8个 | D.1个 |
已知函数 在
在 上是单调函数,则实数的取值范围是( )
上是单调函数,则实数的取值范围是( )
A. |
B. |
C. |
D. |
已知全集 ,集合
,集合 ,则
,则
A. |
B. |
C. |
D. |
给定两个命题p、q,若﹁p是q的必要而不充分条件,则p是﹁q的
| A.充分而不必条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
二维空间中圆的一维测度(周长)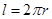 ,二维测度(面积)
,二维测度(面积)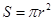 ,观察发现
,观察发现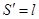 ;三维空间中球的二维测度(表面积)
;三维空间中球的二维测度(表面积)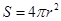 ,三维测度(体积)
,三维测度(体积)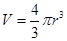 ,观察发现
,观察发现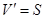 .已知四维空间中“超球”的三维测度
.已知四维空间中“超球”的三维测度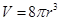 ,猜想其四维测度
,猜想其四维测度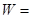 ________.
________.
已知 且满足
且满足 ,则
,则 的最小值为
的最小值为
在复平面内,记复数 对应的向量为
对应的向量为 ,若向量
,若向量 绕坐标原点逆时针旋转
绕坐标原点逆时针旋转 得到向量
得到向量 所对应的复数为 .
所对应的复数为 .
过点A(4,1)的圆C与直线 相切于点B(2,1),则圆C的方程为
相切于点B(2,1),则圆C的方程为
已知函数 .
.
(Ⅰ)当 时,求
时,求 在区间
在区间 上的最值;
上的最值;
(Ⅱ)讨论函数 的单调性.
的单调性.
春节期间,某商场决定从3种服装、2种家电、3种日用品中,选出3种商品进行促销活动。
⑴)试求选出的3种商品中至少有一种是家电的概率;
⑵商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高100元,规定购买该商品的顾客有3次抽奖的机会:若中一次奖,则获得数额为 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
己知等比数列 所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列.
(I)求数列 的通项公式;
的通项公式;
(II)数列 的前n项和为
的前n项和为 ,若
,若 ,求实数
,求实数 的值.
的值.