设集合A={x },B={x
},B={x },则A
},则A (
( )=( )
)=( )
A.{x } } |
B.{x } } |
C.{x } } |
D.{x } } |
i是虚数单位,则复数 的实部为( )
的实部为( )
A. 2 2 |
B. 1 1 |
C.1 | D.2 |
设等比数列{ }的公比q=
}的公比q= , 前n项和为
, 前n项和为 ,则
,则 =( )
=( )
| A.5 | B. |
C. |
D. |
下列函数中既不是奇函数,又不是偶函数的是( )
| A.y=x3 | B. |
C. |
D.y=tanx |
设z="2x+y," 其中变量x,y满足条件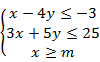 ,若z的最小值为3,则m的值为( )
,若z的最小值为3,则m的值为( )
A.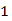 |
B.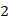 |
C.3 | D.4 |
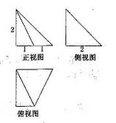
某几何体的三视图如图所示,则其侧面的直角三角形的个数为( )
A.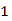 |
B. |
C.3 | D.4 |
已知y=sin(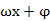 )(
)(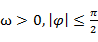 )在区间[0,1]上是单调函数,其图像经过P1(
)在区间[0,1]上是单调函数,其图像经过P1(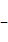 1,0),P2(0,1),则此函数的最小正周期T及
1,0),P2(0,1),则此函数的最小正周期T及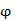 的值分别为( )
的值分别为( )
A.T=4,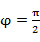 |
B.T=4,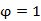 |
C.T=4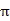 , ,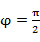 |
D.T=4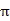 , ,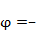 1 1 |
若某射击手每次射击击中目标的概率为P(0<P<1),每次射击的结果相互独立,在他连续8次射击中,“恰有3次击中目标”的概率是“恰有5次击中目标”的概率的 ,则P的值为( )
,则P的值为( )
A. |
B. |
C.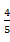 |
D. |
一个算法的程序框图如图所示,如果输入的x的值为2014,则输出的i的结果为( )
A.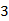 |
B. |
C.6 | D.8 |

直线 经过抛物线y2=4x的焦点,且与抛物线交于A,B两点,若AB的中点横坐标为3,则线段AB的长为( )
经过抛物线y2=4x的焦点,且与抛物线交于A,B两点,若AB的中点横坐标为3,则线段AB的长为( )
A. |
B. |
C.7 | D.8 |
已知在△ABC中,AB=1,BC= ,AC=2,点O为△ABC的外心,若
,AC=2,点O为△ABC的外心,若 =s
=s ,则有序实数对(s,t)为( )
,则有序实数对(s,t)为( )
A. |
B. |
C. |
D. |
已知函数f(x)=ln(ex-1)(x>0)( )
| A.若f(a)+2a=f(b)+3b,则a>b |
| B.若f(a)+2a=f(b)+3b,则a<b |
| C.若f(a)-2a=f(b)-3b,则a>b |
| D.若f(a)-2a=f(b)-3b,则a<b |
(3x+ )6的展开式中常数项为 (用数字作答).
)6的展开式中常数项为 (用数字作答).
中心在坐标原点,焦点在y轴上的双曲线的渐近线过点P(2,1),其离心率为 .
设数列 是公差为1的等差数列,且a1=2,则数列{lgan}的前9项和
是公差为1的等差数列,且a1=2,则数列{lgan}的前9项和
为 .
已知正方体ABCD-A1B1C1D1的棱长为1,点P是线段A1C1上的动点,则四棱锥P-ABCD的外接球半径R的取值范围是 .
已知△ABC中,a,b,c分别为角A,B,C的对边,a2+b2<c2,且sin(2C- )=
)=
(1)求角C的大小;
(2)求 的取值范围。
的取值范围。
如图,正方体ABCD-A1B1C1D1中,E是AB的中点.
(1)在B1C上是否存在点P,使PB∥平面B1ED,若存在,求出点P的位置,若不存在,请说明理由;
(2)求二面角D-B1E-C的平面角的余弦值.
某市共有100万居民的月收入是通过“工资薪金所得”得到的,如图是抽样调查后得到的工资薪金所得X的频率分布直方图。工资薪金个人所得税税率表如表所示。表中“全月应纳税所得额”是指“工资薪金所得”减去3500元所超出的部分(3500元为个税起征点,不到3500元不缴税)。
工资个税的计算公式为:“应纳税额”=“全月应纳税所得额”乘以“适用税率”减去“速算扣除数”。
| 全月应纳税所得额 |
适用税率(%) |
速算扣除数 |
| 不超过1500元 |
3 |
0 |
| 超过1500元至4500元 |
10 |
105 |
| 超过4500元至9000元 |
20 |
555 |
| … |
… |
… |
例如:某人某月“工资薪金所得”为5500元,则“全月应纳税所得额”为5500-3500=2000元,应纳税额为2000 10%-105=95(元)
10%-105=95(元)
在直方图的工资薪金所得分组中,以各组的区间中点值代表该组的各个值,工资薪金所得落入该区间的频率作为x取该区间中点值的概率
(1)试估计该市居民每月在工资薪金个人所得税上缴纳的总税款;
(2)设该市居民每月从工资薪金所得交完税后,剩余的为其月可支配额y(元),试求该市居民月可支配额y的数学期望。
已知直线x+y-1=0经过椭圆C:  的顶点和焦点F.
的顶点和焦点F.
(1)求此椭圆的标准方程;
(2)斜率为k,且过点F的动直线 与椭圆C交于A,B两点,点A关于x轴的对称点为D,求证:直线BD过顶点.
与椭圆C交于A,B两点,点A关于x轴的对称点为D,求证:直线BD过顶点.
已知函数f(x)=ex-e-x(x R)
R)
(1)求证:当x≥0时, ;
;
(2)试讨论函数H(x)=f(x)-ax(x R)的零点个数.
R)的零点个数.
如图,AB是⊙O的一条直径,过A作⊙O的切线,在切线上取一点C,使AC=AB,连接OC,与⊙O交于点D,BD的延长线与AC交于点E,求证:
(1)∠CDE = ∠DAE
(2)AE = CD
已知曲线C的极坐标方程为 =2,以极点为原点,极轴为x轴的正半轴建立直角坐标系,P是曲线C上的动点,点A(2,0),M是线段AP的中点。
=2,以极点为原点,极轴为x轴的正半轴建立直角坐标系,P是曲线C上的动点,点A(2,0),M是线段AP的中点。
(1)求点M轨迹的直角坐标方程;
(2)求证点M到点E( ,0)、F(3、0)的距离之比是常数。
,0)、F(3、0)的距离之比是常数。
已知关于x的不等式 的解集不是空集.
的解集不是空集.
(1)求参数m的取值范围的集合M;
(2)设a,b M,求证:a+b<ab+1.
M,求证:a+b<ab+1.