设i为虚数单位,则 等于
等于
| A.1-i | B.1+i | C.-1+i | D.-1-i |
设集合 ,
, ,则
,则 等于
等于
A. |
B. |
C. |
D. |
设 为平面,a、b为两条不同的直线,则下列叙述正确的是
为平面,a、b为两条不同的直线,则下列叙述正确的是
A.若a∥ ,b∥ ,b∥ ,则a∥b ,则a∥b |
B.若a⊥ ,a∥b,则b⊥ ,a∥b,则b⊥ |
C.若a⊥ ,a⊥b,则b∥ ,a⊥b,则b∥ |
D.若a∥ ,a⊥b,则b⊥ ,a⊥b,则b⊥ |
抛物线y=-x2的准线方程为
A.x= |
B.x= |
C.y= |
D.y= |
已知向量 =(-1,1),
=(-1,1), =(2,x),若
=(2,x),若 ⊥(
⊥( +
+ ),则实数x的值为
),则实数x的值为
| A.0 | B.1 | C.2 | D.4 |
在等比数列{an}中,若a2•a4•a12=64,则a6等于
| A.1 | B.2 | C.3 | D.4 |
已知f(x)是定义在R上的奇函数,且当x<0时,f(x)=3x,则f(log32)的值为
| A.-2 | B. |
C. |
D.2 |
关于函数f(x)=sinx(sinx-cosx)的叙述正确的是
| A.f(x)的最小正周期为2π |
B.f(x)在 内单调递增 内单调递增 |
C.f(x)的图像关于 对称 对称 |
D.f(x)的图像关于 对称 对称 |
如图,一个几何体的三视图(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为
| A.π | B.2π | C.3π | D.4π |
已知实数x,y满足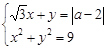 ,则不等式
,则不等式 成立的概率是
成立的概率是
A.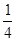 |
B. |
C.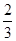 |
D.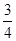 |
已知 ,则
,则 等于________.
等于________.
执行如图程序,当输入42,27时,输出的结果是________.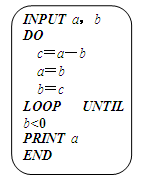
若实数x,y满足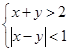 ,则
,则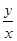 的取值范围是________.
的取值范围是________.
从总体中随机抽出一个容量为20的样本,其数据的分组及各组的频数
如下表,试估计总体的中位数为________.
| 分 组 |
[12,16) |
[16,20) |
[20,24) |
[24,28) |
| 频 数 |
4 |
8 |
5 |
3 |
已知函数 ,下列关于函数
,下列关于函数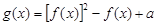 (其中a为常数)的叙述中:
(其中a为常数)的叙述中:
① a>0,函数g(x)至少有4个零点;
a>0,函数g(x)至少有4个零点;
②当a=0时,函数g(x)有5个不同零点;
③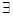 a∈R,使得函数g(x)有6个不同零点;
a∈R,使得函数g(x)有6个不同零点;
④函数g(x)有8个不同零点的充要条件是0<a<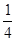 .其中真命题有________.(把你认为的真命题的序号都填上)
.其中真命题有________.(把你认为的真命题的序号都填上)
在四边形ABCD中,AD⊥CD,AD=5,AB=7,∠BDA=60º,∠CBD=15º,求BC长.

盒子中装有形状、大小完全相同的五张卡片,分别标有数字1,2,3,4,5.现从中任意抽出三张.
(1)求三张卡片所标数字之和能被3整除的概率;
(2)求三张卡片所标数字之积为偶数的条件下,三张卡片数字之和为奇数的概率.
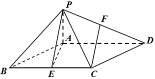
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60º,又PA⊥底面ABCD,E为BC的中点.
(1)求证:AD⊥PE;
(2)设F是PD的中点,求证:CF∥平面PAE.
(本小题12分)设等差数列{an}的前n项和为Sn,已知S3=a6,S8=S5+21.
(1)求Sn的表达式;
(2)求证: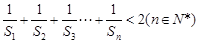 .
.
已知A、B是椭圆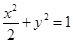 上的两点,且
上的两点,且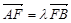 ,其中F为椭圆的右焦点.
,其中F为椭圆的右焦点.
(1)当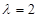 时,求直线AB的方程;
时,求直线AB的方程;
(2)设点 ,求证:当实数
,求证:当实数 变化时,
变化时,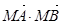 恒为定值.
恒为定值.
已知函数f(x)=x(x+a)-lnx,其中a为常数.
(1)当a=-1时,求f(x)的极值;
(2)若f(x)是区间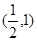 内的单调函数,求实数a的取值范围;
内的单调函数,求实数a的取值范围;
(3)过坐标原点可以作几条直线与曲线y=f(x)相切?请说明理由.