已知集合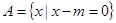 ,
, ,若
,若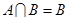 ,则
,则 等于( )
等于( )
| A.1 | B.0或1 | C.﹣1或1 | D.0或1或﹣1 |
已知函数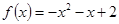 ,则函数
,则函数 的图象是( )
的图象是( )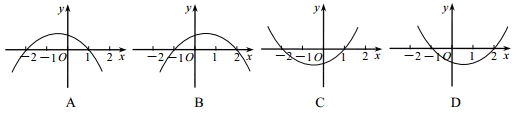
水以匀速注入如图容器中,试找出与容器对应的水的高度 与时间
与时间 的函数关系图象( )
的函数关系图象( )
准线为 的抛物线的标准方程是( )
的抛物线的标准方程是( )
| A.y2=﹣4x | B.y2=﹣8x | C.y2=4x | D.y2=8x |
已知 ,则
,则 的最小值为( )
的最小值为( )
| A.8 | B.6 | C. |
D. |
下列说法正确的是( )
A.“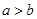 ”是“ ”是“ ”的必要条件 ”的必要条件 |
| B.自然数的平方大于0 |
| C.存在一个钝角三角形,它的三边长均为整数 |
D.“若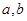 都是偶数,则 都是偶数,则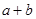 是偶数”的否命题为真 是偶数”的否命题为真 |
若函数 在(0,1)内有极小值,则( )
在(0,1)内有极小值,则( )
A.0< <1 <1 |
B. <1 <1 |
C. >0 >0 |
D. < < |
不等式 的解集是( )
的解集是( )
A.( ,+ ,+ ) ) |
B.(3,+ ) ) |
C.(﹣ ,﹣3)∪(4,+ ,﹣3)∪(4,+ ) ) |
D.(﹣ ,﹣3)∪( ,﹣3)∪( ,+ ,+ ) ) |
下列图象表示的函数能用二分法求零点的是( )
已知函数 ,若
,若 ,且
,且 ,使得
,使得 .则实数
.则实数 的取值范围是( )
的取值范围是( )
A.(﹣ ,1) ,1) |
B.(1, ) ) |
C.(1, ) ) |
D.(﹣ ,1)∪( ,1)∪( ,+ ,+ ) ) |
 是函数
是函数 为偶函数的 _________ 条件.
为偶函数的 _________ 条件.
已知一辆轿车在公路上作加速直线运动,设 s时的速度为
s时的速度为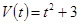 (m/s),则
(m/s),则 =3s时轿车的瞬时加速度为_________ m/s2
=3s时轿车的瞬时加速度为_________ m/s2
若 ,
, ,
, ,则从小到大的顺序为 _________.
,则从小到大的顺序为 _________.
已知函数 的图象在点
的图象在点 处的切线斜率为1,则
处的切线斜率为1,则 .
.
已知正数 ,
, 满足
满足 ,,则
,,则 的最小值为 _________ .
的最小值为 _________ .
.给出定义:若函数 在
在 上可导,即
上可导,即 存在,且导函数
存在,且导函数 在
在 上也可导,则称
上也可导,则称 在
在 上存在二阶导函数,记
上存在二阶导函数,记 .若
.若 在
在 上恒成立,则称f(x)在
上恒成立,则称f(x)在 上为凸函数.以下四个函数在
上为凸函数.以下四个函数在 上不是凸函数的是 _________ .(把你认为正确的序号都填上)
上不是凸函数的是 _________ .(把你认为正确的序号都填上)
① ;
;
② ;
;
③ ;
;
④ .
.
我们把离心率 的双曲线
的双曲线 称为黄金双曲线.如图是双曲线
称为黄金双曲线.如图是双曲线 的图象,给出以下几个说法:
的图象,给出以下几个说法:
①双曲线 是黄金双曲线;
是黄金双曲线;
②若 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
③若 为左右焦点,
为左右焦点, 为左右顶点,
为左右顶点, (0,
(0, ),
), (0,﹣
(0,﹣ )且
)且 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;
④若 经过右焦点
经过右焦点 且
且 ,
, ,则该双曲线是黄金双曲线.
,则该双曲线是黄金双曲线.
其中正确命题的序号为 _________ .
已知 :
: ,
, :函数
:函数 存在极大值和极小值,求使“
存在极大值和极小值,求使“ ”为真命题的
”为真命题的 的取值范围.
的取值范围.
已知 ,不等式
,不等式 的解集
的解集
(Ⅰ)求 的值;
的值;
(Ⅱ)若 恒成立,求
恒成立,求 的取值范围.
的取值范围.
设 ,其中
,其中 为常数.
为常数.
(1)求曲线 (x)在点(4,2)处的切线方程;
(x)在点(4,2)处的切线方程;
(2)如果函数 (x)的图象也经过点(4,2),求
(x)的图象也经过点(4,2),求 (x)与(1)中的切线的交点.
(x)与(1)中的切线的交点.
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤
(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤ ≤200时,车流速度
≤200时,车流速度 是车流密度
是车流密度 的一次函数.
的一次函数.
(Ⅰ)当0≤ ≤200时,求函数
≤200时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时
 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).
已知椭圆 :
: 的离心率为
的离心率为 ,一条准线
,一条准线 .
.
(1)求椭圆 的方程;
的方程;
(2)设 为坐标原点,
为坐标原点, 是
是 上的点,
上的点, 为椭圆
为椭圆 的右焦点,过点
的右焦点,过点 作
作 的垂线与以
的垂线与以 为直径的圆
为直径的圆 交于
交于 两点.
两点.
①若 =
= ,求圆
,求圆 的方程;
的方程;
②若 是
是 上的动点,求证:点
上的动点,求证:点 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.