命题“对所有实数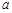 ,都有
,都有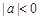 ”的否定是 .
”的否定是 .
设复数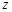 满足
满足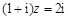 (
(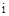 为虚数单位),则
为虚数单位),则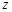 的共轭复数
的共轭复数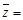 .
.
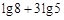 的值是 .
的值是 .
若集合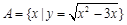 ,集合
,集合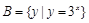 ,则
,则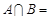 .
.
已知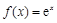 ,若
,若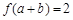 ,则
,则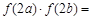 .
.
已知复数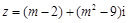 在复平面内对应的点位于第四象限,则实数
在复平面内对应的点位于第四象限,则实数 的取值范围是 .
的取值范围是 .
已知函数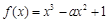 在区间
在区间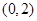 上是单调减函数,则实数
上是单调减函数,则实数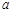 的取值范围是 .
的取值范围是 .
若x,y满足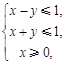 则
则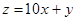 的最大值是 .
的最大值是 .
已知函数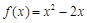 在定义域
在定义域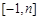 上的值域为
上的值域为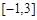 ,则实数
,则实数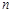 的取值范围是 .
的取值范围是 .
已知一元二次不等式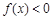 的解集为
的解集为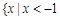 或
或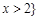 ,则
,则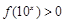 的解集为 .
的解集为 .
若关于x的方程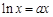 有两个不同实数解,则实数
有两个不同实数解,则实数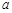 的取值范围是 .
的取值范围是 .
已知定义域为R的函数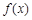 为偶函数,满足
为偶函数,满足 ,且当
,且当 时,
时,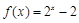 ,则
,则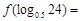 .
.
已知函数 有零点,则
有零点,则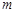 的取值范围是 .
的取值范围是 .
集合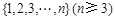 中,每两个相异数作乘积,将所有这些乘积的和记为
中,每两个相异数作乘积,将所有这些乘积的和记为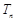 ,如:
,如: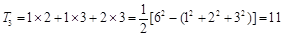 ;
;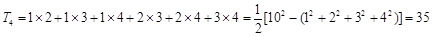 ;
;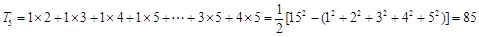
则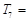 .(写出计算结果)
.(写出计算结果)
已知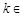 R且
R且 ,直线
,直线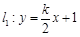 和
和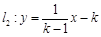 .
.
(1)求直线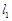 ∥
∥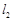 的充要条件;
的充要条件;
(2)当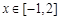 时,直线
时,直线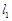 恒在x轴上方,求
恒在x轴上方,求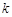 的取值范围.
的取值范围.
(本小题满分14分)
先解答(1),再通过结构类比解答(2):
(1)求证: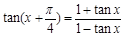 ;
;
(2)设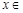 R,a为非零常数,且
R,a为非零常数,且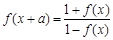 ,试问:
,试问: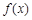 是周期函数吗?证明你的结论.
是周期函数吗?证明你的结论.
已知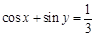 ,x,y
,x,y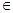 R.
R.
(1)若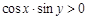 ,求
,求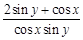 的最小值;
的最小值;
(2)设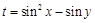 ,求
,求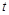 的取值范围.
的取值范围.
已知二次函数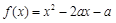 (
(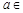 R).
R).
(1)解不等式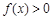 ;
;
(2)函数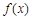 在
在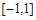 上有零点,求
上有零点,求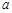 的取值范围.
的取值范围.
已知函数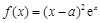 ,
, ,其中
,其中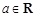 .
.
(1)当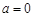 时,求曲线
时,求曲线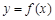 在点
在点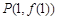 处的切线方程;
处的切线方程;
(2)若存在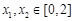 ,使得
,使得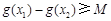 成立,求实数M的最大值;
成立,求实数M的最大值;
(3)若对任意的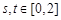 ,都有
,都有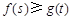 ,求实数
,求实数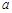 的取值范围.
的取值范围.