设集合 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
直线 在
在 轴上的截距是( )
轴上的截距是( )
A.1  |
B. |
C. |
D. |
下列说法中错误的是( )
| A.经过两条平行直线,有且只有一个平面 |
| B.两两相交且不共点的三条直线确定一个平面 |
C.平面 与平面 与平面 相交,它们只有有限个公共点 相交,它们只有有限个公共点 |
| D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
下列函数中,在区间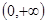 上为增函数的是( )
上为增函数的是( )
A.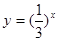 |
B.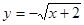 |
C.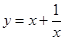 |
D.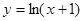 |
直线 和
和 垂直,则实数
垂直,则实数 ( )
( )
A.3  |
B. |
C.1 | D. |
若函数 是函数
是函数
 且
且 的反函数,其图像经过点
的反函数,其图像经过点 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
如图,三棱锥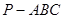 中,
中,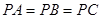 ,
,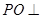 面
面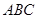 ,垂足为
,垂足为 ,则点
,则点 是
是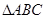 的( )
的( )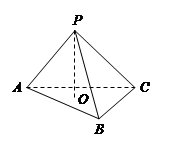
| A.内心 | B.外心 | C.重心 | D.垂心 |
已知函数 ,则
,则 ( )
( )
A.0  |
B.1 | C.2 | D.3 |
已知 是平面,
是平面, 是直线,且
是直线,且

 ,
, 平面
平面 ,则
,则 与平面
与平面 的位置关系是( )
的位置关系是( )
A. 平面 平面 |
B. 平面 平面 |
C. 平面 平面 |
D. 与平面 与平面 相交但不垂直 相交但不垂直 |
设函数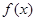 和
和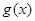 分别是R上的偶函数和奇函数,则下列结论恒成立的是( )
分别是R上的偶函数和奇函数,则下列结论恒成立的是( )
A.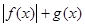 是偶函数 是偶函数 |
B.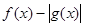 是奇函数 是奇函数 |
C.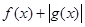 是偶函数 是偶函数 |
D.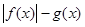 是奇函数 是奇函数 |
函数 的定义域是 .
的定义域是 .
直线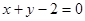 和
和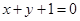 间的距离是 .
间的距离是 .
若幂函数的图象经过点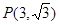 ,那么这个函数的解析式是 .
,那么这个函数的解析式是 .
如图是正方体的平面展开图,那么在这个正方体中,异面直线 与
与 所成的角的大小是 .
所成的角的大小是 .
已知集合 ,集合
,集合 .
.
(1)求 ;
;
(2)求 ;
;
(3)求
如图所示,一个空间几何体的正视图,侧视图,俯视图为全等的等腰直角三角形,,如果直角三角形的直角边边长都为1.
(1)画出几何体的直观图(不要求写出做图过程);
(2)求几何体的表面积和体积
求经过直线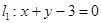 与直线
与直线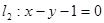 的交点M,且分别满足下列条件的直线方程:
的交点M,且分别满足下列条件的直线方程:
(1)与直线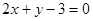 平行;
平行;
(2)与直线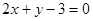 垂直.
垂直.
如图,正方形 的边长为1,正方形
的边长为1,正方形 所在平面与平面
所在平面与平面 互相垂直,
互相垂直, 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
已知函数 , 其中
, 其中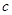 为常数,且函数
为常数,且函数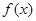 图像过原点.
图像过原点.
求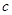 的值;
的值;
(1)证明:函数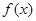 在[0,2]上是单调递增函数;
在[0,2]上是单调递增函数;
(2)已知函数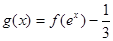 , 求g(x)≥0时x的取值范围。.
, 求g(x)≥0时x的取值范围。.
已知二次函数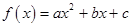 .
.
(1)若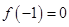 ,试判断函数
,试判断函数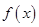 零点个数
零点个数
(2)若对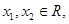 且
且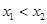 ,
,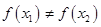 ,证明方程
,证明方程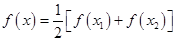 必有一个实数根属于
必有一个实数根属于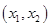 。
。
(3)是否存在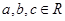 ,使
,使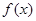 同时满足以下条件①当
同时满足以下条件①当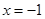 时, 函数
时, 函数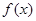 有最小值0;;②对任意实数x,都有
有最小值0;;②对任意实数x,都有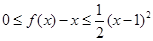 。若存在,求出
。若存在,求出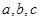 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。