在空间直角坐标系中，点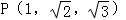
，过点P作平面xOy的垂线PQ，则Q的坐标为（ ）
A． |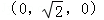
B． |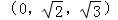
C． |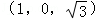
D． |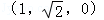
已知点A（﹣3，1，﹣4），则点A关于x轴的对称点的坐标为（ ）
| A．（﹣3，﹣1，4） | B．（﹣3，﹣1，﹣4） |
| C．（3，1，4） | D．（3，﹣1，﹣4） |
已知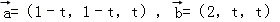
，则
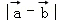的最小值是（ ）
A． |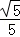
B． |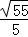
C． |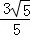
D． |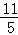
下列各点不在曲线x2+y2+z2=12上的是（ ）
| A．（2，﹣2，2） | B． |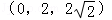
| C．（﹣2，2，2） | D．（1，3，4） |
坐标原点到下列各点的距离最小的是（ ）
| A．（1，1，1） | B．（1，2，2） | C．（2，﹣3，5） | D．（3，0，4） |
已知A点坐标为A（1，1，1），B（3，3，3），点P在x轴上，且|PA|=|PB|，则P点坐标为（ ）
| A．（6，0，0） | B．（6，0，1） | C．（0，0，6） | D．（0，6，0） |
点（2，0，3）在空间直角坐标系中的位置是在（ ）
| A．y轴上 | B．xOy平面上 | C．xOz平面上 | D．第一卦限内 |
已知两点M1（﹣1，0，2），M2（0，3，﹣1），此两点间的距离为（ ）
A． |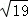
B． |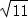
C．19 | D．11 |
若向量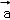
在y轴上的坐标为0，其他坐标不为0，那么与向量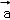平行的坐标平面是（ ）
| A．xOy平面 | B．xOz平面 | C．yOz平面 | D．以上都有可能 |
在z轴上与点A（﹣4，1，7）和点B（3，5，﹣2）等距离的点C的坐标为 ．
已知三角形A（2，﹣1，4），B（3，2，﹣6），C（5，0，2），则①过A点的中线长为 ；②过B点的中线长为 ；③过C点的中线长为 ．
在空间直角坐标系O﹣xyz中，z=1的所有点构成的图形是 ．点P（2，3，5）到平面xOy的距离为 ．
已知点A（1，2，1），B（﹣1，3，4），D（1，1，1），若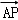
=2
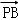，则|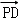
|的值是 ．
点P（﹣3，2，﹣1）关于平面xOy的对称点是 ，关于平面yOz的对称点是 ，关于平面zOx的对称点是 ，关于x轴的对称点是 ，关于y轴的对称点是 ，关于z轴的对称点是 ．
点M（4，﹣3，5）到原点的距离d= ，到z轴的距离d= ．
在空间直角坐标系中，在Ox轴上的点P1的坐标特点为 ，在Oy轴上的点P2的坐标特点为 ，在Oz轴上的点P3的坐标特点为 ，在xOy平面上的点P4的坐标特点为 ，在yOz平面上的点P5的坐标特点为 ，在xOz平面上的点P6的坐标特点为 ．
已知空间三点的坐标为A（1，5，﹣2），B（2，4，1），C（p，3，q+2），若A，B，C三点共线，则p= ，q= ．
求到两定点A（2，3，0），B（5，1，0）距离相等的点的坐标（x，y，z）满足的条件．
给定空间直角坐标系，在x轴上找一点P，使它与点P0（4，1，2）的距离为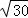
．
求证：以A（﹣4，﹣1，﹣9），B（﹣10，1，﹣6），C（﹣2，﹣4，﹣3）为顶点的三角形是等腰直角三角形．
如图，长方体OABC﹣D'A'B'C'中，|OA|=3，|OC|=4，|OD'|=3，A'C'于B'D'相交于点P．分别写出C，B'，P的坐标．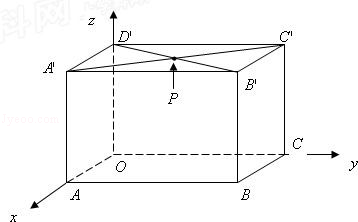
在xOy平面内的直线x+y=1上确定一点M；使M到点N（6，5，1）的距离最小．
试解释方程（x﹣12）2+（y+3）2+（z﹣5）2=36的几何意义．
已知点P的坐标为（3，4，5），试在空间直角坐标系中作出点P．