已知集合A={x∈Z|x2-1≤0},B={x|x2-x-2=0},则A∩B=( )
| A.∅ | B.{2} | C.{0} | D.{-1} |
下列说法中正确的是( )
A.命题“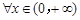 , ,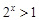 ”的否定是“ ”的否定是“ , , ≤1” ≤1” |
B.命题“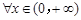 , ,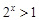 ”的否定是“ ”的否定是“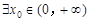 , , ≤1” ≤1” |
C.命题“若 ,则 ,则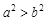 ”的逆否命题是“若 ”的逆否命题是“若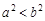 ,则 ,则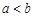 ” ” |
D.命题“若 ,则 ,则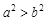 ”的逆否命题是“若 ”的逆否命题是“若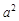 ≥ ≥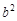 ,则 ,则 ≥ ≥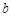 ” ” |
设各项均不为0的数列{an}满足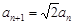 (n≥1),Sn是其前n项和,若
(n≥1),Sn是其前n项和,若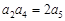 ,则S4=( )
,则S4=( )
A.4 |
B.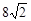 |
C. |
D. |
如图,正六边形ABCDEF的边长为1,则 =( )
=( )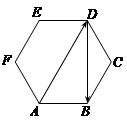
| A.-3 | B.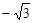 |
C.3 | D. |
已知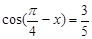 ,那么
,那么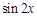 =( )
=( )
A.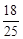 |
B. |
C.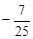 |
D.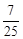 |
已知x,y满足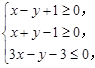 则2x-y的最大值为m]( )
则2x-y的最大值为m]( )
| A.1 | B.2 | C.3 | D.4 |
已知x∈[-π,π],则“x∈ ”是“sin(sinx)<cos(cosx)成立”的( )
”是“sin(sinx)<cos(cosx)成立”的( )
| A.充要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
 是定义在非零实数集上的函数,
是定义在非零实数集上的函数, 为其导函数,且
为其导函数,且 时,
时, ,记
,记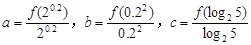 ,则 ( )
,则 ( )
A.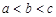 |
B. |
C.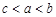 |
D. |
已知函数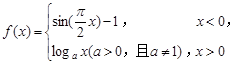 的图象上关于
的图象上关于 轴对称的点至少有3对,则实数
轴对称的点至少有3对,则实数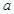 的取值范围是( )
的取值范围是( )
A. |
B.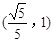 |
C. |
D.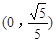 |
已知 R,且
R,且 ≥
≥ 对x∈R恒成立,则
对x∈R恒成立,则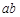 的最大值是( )
的最大值是( )
A. |
B.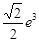 |
C.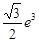 |
D.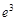 |
若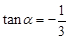 ,则
,则 _______.
_______.
已知向量a=(1,2),b=(2,0),若向量λa+b与向量c=(1,-2)共线,则实数λ=______.
某商场销售某种商品的经验表明,该产品生产总成本C与产量q(q∈N*)的函数关系式为C=100+4q,销售单价p与产量q的函数关系式为 .要使每件产品的平均利润最大,则产量q等于_______.
.要使每件产品的平均利润最大,则产量q等于_______.
已知函数f(x)= ,则f(
,则f( )+f(
)+f( )+f(
)+f( )+…+f(
)+…+f( )=______.
)=______.
定义:如果函数 在定义域内给定区间
在定义域内给定区间 上存在
上存在 ,满足
,满足 ,则称函数
,则称函数 是
是 上的“平均值函数”,
上的“平均值函数”, 是它的一个均值点.例如y=| x |是
是它的一个均值点.例如y=| x |是 上的“平均值函数”,0就是它的均值点.给出以下命题:
上的“平均值函数”,0就是它的均值点.给出以下命题:
①函数 是
是 上的“平均值函数”.
上的“平均值函数”.
②若 是
是 上的“平均值函数”,则它的均值点x0≥
上的“平均值函数”,则它的均值点x0≥ .
.
③若函数 是
是 上的“平均值函数”,则实数m的取值范围是
上的“平均值函数”,则实数m的取值范围是 .
.
④若 是区间[a,b] (b>a≥1)上的“平均值函数”,
是区间[a,b] (b>a≥1)上的“平均值函数”, 是它的一个均值点,则
是它的一个均值点,则 .
.
其中的真命题有 .(写出所有真命题的序号)
已知向量m=(sinωx,cosωx),n=(cosωx,cosωx),其中ω>0,函数 2m·n-1的最小正周期为π.
2m·n-1的最小正周期为π.
(1)求ω的值;
(2)求函数 在[
在[ ,
, ]上的最大值.
]上的最大值.
已知函数f (t)=log2(2-t)+ 的定义域为D.
的定义域为D.
(1)求D;
(2)若函数g (x)=x2+2mx-m2在D上存在最小值2,求实数m的值.
在△ABC中,a,b,c分别是内角A,B,C的对边,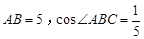 .
.
(1)若 ,求
,求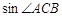 的值;
的值;
(2)若 是边
是边 中点,且
中点,且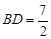 ,求边
,求边 的长.
的长.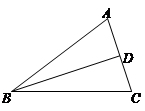
记公差不为0的等差数列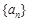 的前
的前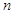 项和为
项和为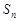 ,
, ,
,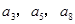 成等比数列.
成等比数列.
(1)求数列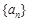 的通项公式
的通项公式 及
及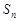 ;
;
(2)若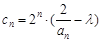 ,n=1,2,3,…,问是否存在实数
,n=1,2,3,…,问是否存在实数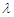 ,使得数列
,使得数列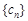 为单调递减数列?若存在,请求出
为单调递减数列?若存在,请求出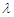 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数f(x)=ex-ax-1(e为自然对数的底数),a>0.
(1)若函数f(x)恰有一个零点,证明:aa=ea-1;
(2)若f(x)≥0对任意x∈R恒成立,求实数a的取值集合.
已知函数 (m,n为常数,
(m,n为常数,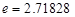 …是自然对数的底数),曲线
…是自然对数的底数),曲线 在点
在点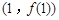 处的切线方程是
处的切线方程是 .
.
(1)求m,n的值;
(2)求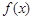 的单调区间;
的单调区间;
(3)设 (其中
(其中 为
为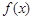 的导函数),证明:对任意
的导函数),证明:对任意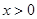 ,
, .
.