设集合U={1,2,3,4},A={1,2},B={2,4},则 等于( )
等于( )
| A.{1,4} | B.{1,3,4} | C.{2} | D.{3} |
已知复数z 满足 ,则
,则 ( )
( )
A. |
B. |
C. |
D.2 |
点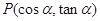 在第二象限是角
在第二象限是角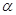 的终边在第三象限的( )
的终边在第三象限的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 是两个不同的平面,
是两个不同的平面,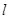 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若 ,则 ,则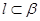 |
B.若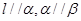 ,则 ,则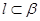 |
C.若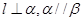 ,则 ,则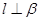 |
D.若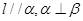 ,则 ,则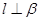 |
已知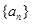 是等差数列,其前
是等差数列,其前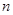 项和为
项和为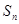 ,若
,若 ,则
,则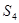 =( )
=( )
| A.15 | B.14 | C.13 | D.12 |
已知向量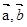 满足
满足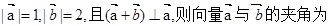 ( )
( )
A.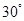 |
B.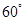 |
C. |
D.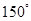 |
同时具有性质“①最小正周期是 ,②图象关于直线
,②图象关于直线 对称”的一个函数是 ( )
对称”的一个函数是 ( )
A. |
B. |
C. |
D. |
x,y满足约束条件 若
若 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数 的值为( )
的值为( )
A. 或-1 或-1 |
B.2或 |
C.2或1 | D.2或-1 |
已知函数 当
当 时,
时, 有解,则实数
有解,则实数 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. |
已知椭圆 与圆
与圆 ,若在椭圆
,若在椭圆 上不存在点
上不存在点 ,使得由点
,使得由点 所作的圆
所作的圆 的两条切线互相垂直,则椭圆
的两条切线互相垂直,则椭圆 的离心率的取值范围是( )
的离心率的取值范围是( )
A. |
B. |
C. |
D. |
已知角 的终边经过点
的终边经过点 ,则
,则
 =__________.
=__________.
某几何体的三视图如图所示,则该几何体的体积为____________.
设 ,则
,则 的值为 .
的值为 .
设直线过点 其斜率为1,且与圆
其斜率为1,且与圆 相切,则
相切,则 的值为________.
的值为________.
函数 的定义域为______________.
的定义域为______________.
已知 ,若
,若 ,则
,则 .
.
已知 为偶函数,当
为偶函数,当 时,
时, ,则满足
,则满足 的实数
的实数 的个数有________个.
的个数有________个.
(本小题满分14分)已知 为
为 的三个内角
的三个内角 的对边,向量
的对边,向量 ,
, ,
, ,
, ,
,
(1)求角 的大小;(2)求
的大小;(2)求 的值.
的值.
(本小题满分14分)等差数列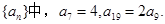 数列
数列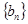 满足
满足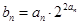
(1)求数列 的通项公式;
的通项公式;
(2)求数列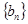 的前
的前 项和
项和 .
.
(本小题满分14分))如图,在三棱柱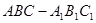 中,
中, ⊥底面
⊥底面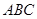 ,且△
,且△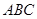 为正三角形,
为正三角形,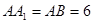 ,
,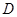 为
为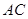 的中点.
的中点.
(1)求证:直线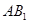 ∥平面
∥平面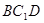 ;
;
(2)求证:平面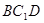 ⊥平面
⊥平面 ;
;
(3)求三棱锥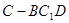 的体积.
的体积.
(本小题满分15分)已知函数 是定义在
是定义在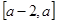 上的偶函数,
上的偶函数,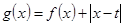 ,其中
,其中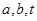 均为常数.
均为常数.
(1)求实数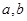 的值;
的值;
(2)试讨论函数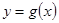 的奇偶性;
的奇偶性;
(3)若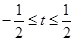 ,求函数
,求函数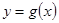 的最小值.
的最小值.
(本小题满分15分)如图,已知抛物线 上点
上点 到焦点
到焦点 的距离为3,直线
的距离为3,直线 交抛物线
交抛物线 于
于 两点,且满足
两点,且满足 。圆
。圆 是以
是以 为圆心,
为圆心, 为直径的圆.
为直径的圆.
(1)求抛物线 和圆
和圆 的方程;
的方程;
(2)设点 为圆
为圆 上的任意一动点,求当动点
上的任意一动点,求当动点 到直线
到直线 的距离最大时的直线方程.
的距离最大时的直线方程.