如果输入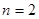 ,那么执行下图中算法后的输出结果是( )
,那么执行下图中算法后的输出结果是( )
A. |
B. |
C.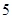 |
D.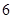 |
已知命题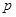 :
: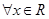 ,
,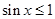 ,则( )
,则( )
A.¬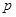 : :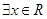 , ,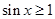 |
B.¬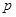 : :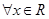 , ,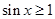 |
C.¬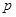 : :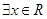 , ,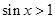 |
D.¬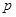 : :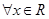 , ,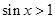 |
某单位有职工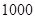 人,其中青年职工
人,其中青年职工 人,中年职工
人,中年职工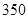 人,老年职工
人,老年职工 人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本容量为20,则样本中的中年职工的容量为( )
人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本容量为20,则样本中的中年职工的容量为( )
| A.4 | B.5 | C.6 | D.7 |
若命题“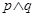 ”为假,且“
”为假,且“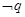 ”为假,则( )
”为假,则( )
A.“ ”为假 ”为假 |
B. 假 假 |
C. 真 真 |
D.不能判断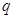 的真假 的真假 |
命题“若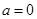 ,则
,则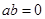 ”的逆否命题是( )
”的逆否命题是( )
A.若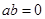 ,则 ,则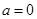 |
B.若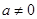 ,则 ,则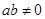 |
C.若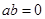 ,则 ,则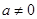 |
D.若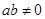 ,则 ,则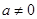 |
某同学设计下面的程序框图用以计算和式 的值,则在判断框中应填写( )
的值,则在判断框中应填写( )
A. ? ? |
B. ? ? |
C. ? ? |
D. ? ? |
已知回归直线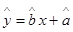 的
的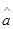 估计值为0.2,样本点的中心为(4,5),则回归直线方程为( )
估计值为0.2,样本点的中心为(4,5),则回归直线方程为( )
A.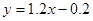 |
B.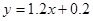 |
C. |
D. |
从装有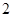 个白球和
个白球和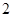 个蓝球的口袋中任取
个蓝球的口袋中任取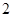 个球,那么对立的两个事件是( )
个球,那么对立的两个事件是( )
| A.“恰有一个白球”与“恰有两个白球” |
| B.“至少有一个白球”与“至少有—个蓝球” |
| C.“至少有—个白球”与“都是蓝球” |
| D.“至少有一个白球”与“都是白球” |
设命题甲:|x-2|<3,命题乙: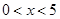 ,那么甲是乙的( )
,那么甲是乙的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
掷两枚骰子,出现点数之和为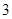 的概率是( )
的概率是( )
A.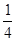 |
B.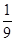 |
C.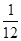 |
D.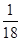 |
下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是( )
游戏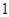 |
游戏 |
游戏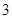 |
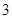 个黑球和 个黑球和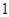 个白球 个白球 |
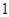 个黑球和 个黑球和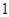 个白球 个白球 |
 个黑球和 个黑球和 个白球 个白球 |
取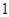 个球,再取 个球,再取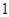 个球 个球 |
取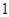 个球 个球 |
取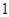 个球,再取 个球,再取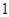 个球 个球 |
| 取出的两个球同色→甲胜 |
取出的球是黑球→甲胜 |
取出的两个球同色→甲胜 |
| 取出的两个球不同色→乙胜 |
取出的球是白球→乙胜 |
取出的两个球不同色→乙胜 |
A.游戏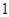 和游戏
和游戏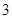 B.游戏
B.游戏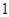 C.游戏
C.游戏 D.游戏
D.游戏
在集合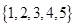 中,任取一个偶数
中,任取一个偶数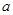 和一个奇数
和一个奇数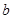 ,构成以原点为起点的向量
,构成以原点为起点的向量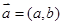 .从所有得到的以原点为起点的向量中,任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为
.从所有得到的以原点为起点的向量中,任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为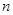 ,其中面积等于
,其中面积等于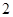 的平行四边形的个数为
的平行四边形的个数为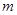 ,则
,则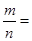 ( )
( )
A.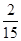 |
B.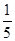 |
C.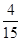 |
D. |
随机抽取某中学 位高三同学,调查他们春节期间购书费用(单位:元),获得数据的茎叶图如图,这
位高三同学,调查他们春节期间购书费用(单位:元),获得数据的茎叶图如图,这 位同学购书费用的中位数是__________.
位同学购书费用的中位数是__________.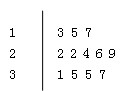
已知 ,当
,当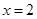 时,用秦九韶算法求
时,用秦九韶算法求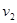 =______________.
=______________.
一段细绳长10cm,把它拉直后随机剪成两段,则两段长度都超过4的概率为__________________.
给出下列结论:
①命题“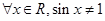 ”的否定是“
”的否定是“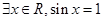 ”;
”;
②命题“有些正方形是平行四边形”的否定是“所有正方形不都是平行四边形”;
③命题“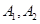 是对立事件”是命题“
是对立事件”是命题“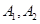 是互斥事件”的充分不必要条件;
是互斥事件”的充分不必要条件;
④若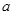 ,
,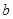 是实数,则“
是实数,则“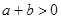 且
且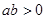 ”是“
”是“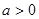 且
且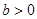 ”的必要不充分条件.
”的必要不充分条件.
其中正确结论的是 _________________.
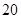 名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
(1)求频率分布直方图中 的值;
的值;
(2)分别求出成绩落在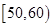 与
与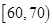 中的学生人数;
中的学生人数;
(3)从成绩在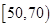 的学生中任选
的学生中任选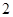 人,求此
人,求此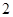 人的成绩都在
人的成绩都在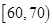 中的概率.
中的概率.
(本小题满分12分)设命题p: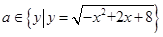 ,命题q:关于
,命题q:关于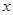 的方程
的方程
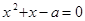 的一根大于1,另一根小于1,命题“
的一根大于1,另一根小于1,命题“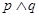 ”为假命题,命题“
”为假命题,命题“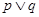 ”为真命题,求实数
”为真命题,求实数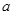 的取值范围.
的取值范围.
给出 个数,
个数,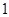 ,
,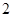 ,
,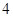 ,
,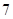 ,
,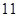 , ,其规律是:第
, ,其规律是:第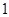 个数是
个数是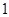 ,第
,第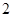 个数比第
个数比第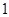 个数大
个数大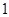 ,第
,第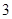 个数比第
个数比第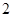 个数大
个数大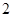 ,第
,第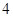 个数比第
个数比第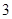 个数大
个数大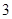 , ,以此类推. 要求计算这
, ,以此类推. 要求计算这 个数的和.(1)画出的程序框图;(2)并用程序语言编程序.(要求详细的程序步骤)
个数的和.(1)画出的程序框图;(2)并用程序语言编程序.(要求详细的程序步骤)
(满分12分)假设关于某设备的使用年限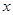 和所支出的维修费用
和所支出的维修费用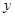 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限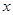 |
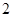 |
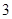 |
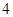 |
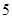 |
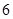 |
维修费用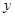 |
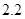 |
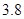 |
 |
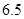 |
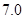 |
若由资料知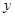 对
对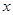 呈线性相关关系。
呈线性相关关系。
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程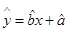 的回归系数
的回归系数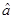 ,
,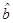 .
.
(3)估计使用年限为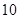 年时,维修费用是多少?
年时,维修费用是多少?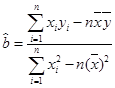 ,
,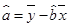
(本小题满分12分) 一个黑色小布袋,袋中有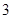 只黄色、
只黄色、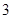 只红色的乒乓球(除颜色外其体积、质地完全相同),从袋中随机摸出
只红色的乒乓球(除颜色外其体积、质地完全相同),从袋中随机摸出 个球,
个球,
(1)求摸出的 个球为红球和摸出的
个球为红球和摸出的 个至少一球为黄球的概率分别是多少?
个至少一球为黄球的概率分别是多少?
(2)求摸出的 个球的颜色不相同的概率是多少?
个球的颜色不相同的概率是多少?
(本小题满分14分)数列 满足:
满足: ;
;
(1)证明:数列 是单调递减数列的充要条件是:
是单调递减数列的充要条件是: ;
;
(2)求 的取值范围,使数列
的取值范围,使数列 是单调递增数列.
是单调递增数列.