已知集合 ={0,1,2,3},
={0,1,2,3}, =
= ,则
,则 =( )
=( )
| A.{0} | B. |
C. |
D.{1,2} |
已知函数 ,则
,则 ( )
( )
| A.1 | B.-2 | C.2 | D. |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
A.向左平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向右平移 个单位长度 个单位长度 |
由曲线 ,直线
,直线 及
及 轴所围成的图形的面积为( )
轴所围成的图形的面积为( )
A. |
B.4 | C. |
D.6 |
在 中,角
中,角 所对的边分别为
所对的边分别为 ,
, 表示
表示 的面积,若
的面积,若 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
若 为实数,则“
为实数,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知函数 的图象大致为( )
的图象大致为( )
已知锐角 满足
满足 ,,则
,,则 = ( )
= ( )
A. |
B. π π |
C. 或 或 π π |
D. |
如果实数 满足不等式组
满足不等式组 ,目标函数
,目标函数 的最大值为6,最小值为0,则实数
的最大值为6,最小值为0,则实数 的值为( )
的值为( )
| A.1 | B.2 | C.3 | D.4 |
定义域为R的函数 ,若对任意两个不相等的实数
,若对任意两个不相等的实数 ,都有
,都有 ,则称函数为“H函数”,现给出如下函数:
,则称函数为“H函数”,现给出如下函数:
① ②
② ③
③ ④
④
其中为“H函数”的有( )
| A.①② | B.③④ | C.②③ | D.①②③ |
已知复数 ,且
,且 是实数,则实数k= .
是实数,则实数k= .
已知角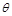 的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,
的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,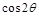 =__________.
=__________.
若两个非零向量 ,
, 满足
满足 ,则向量
,则向量 与
与 的夹角为____.
的夹角为____.
已知定义在 上的函数
上的函数 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的 ,都有
,都有  ;②函数
;②函数 的图象关于
的图象关于 轴对称;③对于任意的
轴对称;③对于任意的 ,且
,且  ,都有
,都有 .则
.则 从小到大排列是________.
从小到大排列是________.
下列4个命题:
①“如果 ,则
,则 、
、 互为相反数”的逆命题
互为相反数”的逆命题
②“如果 ,则
,则 ”的否命题
”的否命题
③在△ABC中,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
④“函数 为奇函数”的充要条件是“
为奇函数”的充要条件是“ ”
”
其中真命题的序号是_________.
(本小题满分12分)已知p:函数 在
在 上单调递增;q:关于
上单调递增;q:关于 的不等式
的不等式 的解集为R.若
的解集为R.若 为真命题,
为真命题, 为假命题,求
为假命题,求 的取值范围.
的取值范围.
(本小题满分12分)函数 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形.
为正三角形.
(1)求 的值及函数
的值及函数 的值域;
的值域;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(本小题满分12分)在三角形ABC中,∠A,∠B,∠C的对边分别为 且
且
(1)求∠A;
(2)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)已知某公司生产品牌服装的年固定成本是10万元,每生产一千件,需另投入2.7万元,设该公司年内共生产该品牌服装 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式
(千件)的函数解析式
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大?
(注:年利润=年销售收入 年总成本)
年总成本)
(本小题满分13分)
(1)求 的单调区间和极值
的单调区间和极值
(2)若 及
及 不等式
不等式 恒成立,求实数
恒成立,求实数 的范围.
的范围.
(本小题满分14分)
设 是函数
是函数 的一个极值点.
的一个极值点.
(1)求 与
与 的关系式(用
的关系式(用 表示
表示 ),并求
),并求 的单调区间;
的单调区间;
(2)设 ,若存在
,若存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.