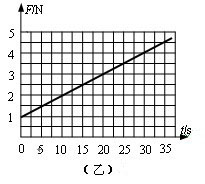
如图(甲)所示，一对平行光滑轨道放置在水平面上，两轨道间距L＝0.20 m，电阻R＝10 W，有一质量为1kg的导体棒平放在轨道上并与两轨道垂直，导体棒及轨道的电阻皆可忽略不计，整个装置处于垂直轨道平面向下的匀强磁场中。现从t=0开始，用一水平向右的外力F沿轨道方向拉动导体棒，使之做初速度为零的匀加速直线运动，F与时间t的关系如图(乙)所示，试求：
（1）导体棒运动的加速度a。
（2）磁场的磁感应强度B。
（3）导体棒运动到第20s时，电阻R的电功率。
（4）若改为恒定拉力作用，但仍要导体棒以该加速度做匀加速运动，在其它条件不变的
情况下，简要说明磁场的磁感应强度必须满足的条件。
一长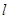
=0.80m的轻绳一端固定在
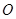点，另一端连接一质量
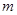=0.10kg的小球，悬点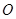距离水平地面的高度H = 1.00m．开始时小球处于
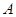点，此时轻绳拉直处于水平方向上，如图所示．让小球从静止释放，当小球运动到
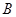点时，轻绳碰到悬点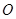正下方一个固定的钉子P时立刻断裂．不计轻绳断裂的能量损失，取重力加速度g=10m/s2． 
（1）绳断裂后球从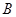点抛出并落在水平地面的C点，求C点与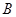点之间的水平距离．
（2）若轻绳所能承受的最大拉力Fm = 9.0N，求钉子P与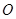点的距离d应满足什么条件？
图示为修建高层建筑常有的塔式起重机．在起重机将质量m＝5×103kg的重物竖直吊起的过程中，重物由静止开始向上作匀加速直线运动，加速度a＝0.2m/s2，当起重机输出功率达到其允许的最大值时，保持该功率直到重物做vm＝1.02m/s的匀速运动．取g＝10m/s2，不计额外功．求：
(1)起重机允许输出的最大功率．
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率．
已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v1的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行周期T。
如图所示，光滑水平面上停着一个质量为M的木块乙，乙上固定着一轻质弹簧，另一个质量为m的木块以速度为
向右运动，求弹簧在压缩过程中所具有的最大弹性势能(设压缩量在弹性限度内)。
如图所示,从AB面射到矩形玻璃砖ABCD的光线,不论入射角i多大,都只能从CD面射出.求玻璃的折射率n的取值范围.