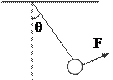
如图所示,用轻绳吊一个重为G的小球,欲施一力F使小球在图示位置平衡(θ<30°), 下列说法正确的是( )
A.力F最小值为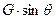 |
| B.若力F与绳拉力大小相等,力F方向与竖直方向必成θ角. |
| C.若力F与G大小相等,力F方向与竖直方向必成θ角. |
| D.若力F与G大小相等,力F方向与竖直方向可成2θ角. |
如图所示,虚线是某一静电场的一簇等势线及其电势值,一带电粒子只在电场力的作用下飞经该电场时,恰能沿图中的实线从A点飞到B点,则下列判断正确的是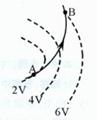
| A.该粒子带负电 |
| B.A点的场强大于B点的场强 |
| C.粒子在A点的电势能大于在B点的电势能 |
| D.粒子在A点的动能小于在B点的动能 |
如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面。设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,不计小球与弹簧碰撞过程中的能量损失,则小球在C点时弹簧的弹性势能为
A. |
B. |
C. |
D. |
如图所示,一木块在垂直于倾斜天花板平面的推力F作用下处于静止状态,则下列判断正确的是
| A.天花板与木块间的弹力可能为零 |
| B.天花板对木块的摩擦力可能为零 |
| C.推力F逐渐增大的过程中,木块将始终保持静止 |
| D.木块受天花板的摩擦力随推力F的增大而变化 |
某位同学为了研究超重和失重现象,将重为50N的物体带到电梯中,并将它放在水平放置的传感器上,电梯由启动到停止的过程中,测得重物的压力随时间变化的图象如图所示。设在t1=2s和t2=8s时电梯的速度分别为v1和v2。下列判断正确的是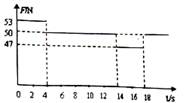
| A.电梯在上升,v1>v2 |
| B.电梯在上升,v2>v1 |
| C.电梯在下降,v1>v2 |
| D.电梯在下降,v2>v1 |
从手中竖直向上抛出的小球,与水平天花板碰撞后又落回到手中,设竖直向上的方向为正方向,小球与天花板碰撞时间极短。若不计空气阻力和碰撞过程中动能的损失,则下列图像中能够描述小球从抛出到落回手中整个过程运动规律的是