如图3-12-6所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态,设拔去销钉M瞬间,小球加速度的大小为12米/秒2,若不拔去销钉M而拔去销钉N瞬间,小球的加速度可能是(取g=10米/秒2)( )
| A.22米/秒2,竖直向上 | B.22米/秒2,竖直向下 |
| C.2米/秒2,竖直向上 | D.2米/秒2,竖直向下 |
一圆盘可绕通过圆盘中心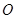 点且垂直于盘面的竖直轴转动,在圆盘上放置一小块木块
点且垂直于盘面的竖直轴转动,在圆盘上放置一小块木块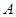 ,它随圆盘一起做匀速圆周运动,如图所示,则关于木块
,它随圆盘一起做匀速圆周运动,如图所示,则关于木块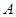 的受力,下列说法正确的是
的受力,下列说法正确的是
A.木块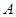 受重力、支持力和向心力 受重力、支持力和向心力 |
B.木块 受重力、支持力和静摩擦力,摩擦力的方向指向圆心 受重力、支持力和静摩擦力,摩擦力的方向指向圆心 |
C.木块 受重力、支持力和静摩擦力,摩擦力的方向与木块运动方向相反 受重力、支持力和静摩擦力,摩擦力的方向与木块运动方向相反 |
D.木块 受重力、支持力和静摩擦力,摩擦力的方向与木块运动方向相同 受重力、支持力和静摩擦力,摩擦力的方向与木块运动方向相同 |
关于不在同一直线上的两个分运动的合成,下列说法正确的是
| A.两个匀速直线的合运动可能是曲线运动 |
| B.一个匀速直线运动和一个匀变速直线运动的合运动必定是直线运动 |
| C.一个匀速直线运动和一个匀变速直线运动的合运动必定是曲线运动 |
| D.两个匀变速直线运动的合运动必定是直线运动 |
在一段半径为R的圆孤形水平弯道上,已知弯道路面对汽车轮胎的最大静摩擦力等于车重的μ倍,则汽车拐弯时的安全速度是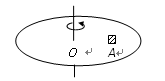
A.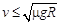 |
B.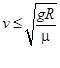 |
C.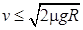 |
D.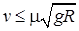 |
在匀速圆周运动中,不变的物理量是
| A.角速度 | B.加速度 |
| C.线速度 | D.作用在物体上的合外力的大小 |
关于平抛运动,下列说法中正确的是
| A.平抛运动都是加速度不变的运动 |
| B.平抛运动的水平射程只决定于初始位置的高低,而与抛出的速度无关[X。X。K] |
| C.平抛运动的水平射程只决定于初速度的大小而与抛出点的高度无关 |
| D.抛体运动的速度和加速度的方向都是在不断变化的 |