(本小题满分12分)数列 中,
中,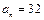 ,
, ,
,
(1)若数列 为公差为11的等差数列,求
为公差为11的等差数列,求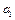 ;
;
(2)若数列 为以
为以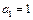 为首项的等比数列,求数列
为首项的等比数列,求数列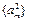 的前m项和
的前m项和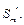

一射手对靶射击,直到第一次命中为止,每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目ξ的期望为( )
| A.2.44 | B.3.376 | C.2.376 | D.2.4 |
已知随机变量X的分布列是:
| X |
4 |
a |
9 |
10 |
| P |
0.3 |
0.1 |
b |
0.2 |
且EX=7.5,则a的值为( )
A.5B.6C.7D.8
设Eξ=10,Eη=3,则E(3ξ+5η)=( )
| A.45 | B.40 | C.35 | D.15 |
下列是4个关于离散型随机变量ξ的期望和方差的描述
①Eξ与Dξ是一个数值,它们是ξ本身所固有的特征数,它们不具有随机性
②若离散型随机变量一切可能取值位于区间内,则a≤Eξ≤b
③离散型随机变量的期望反映了随机变量取值的平均水平,而方差反映的是随机变量取值的稳定与波动,集中与离散的程度
④离散型随机变量的期望值可以是任何实数,而方差的值一定是非负实数
以上4个描述正确的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤4)=0.84,则P(ξ<0)=( )
| A.0.16 | B.0.32 | C.0.68 | D.0.84 |