如图所示,半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为U,两圆之间的空间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出,粒子质量为m,电量为q,(不计粒子重力,忽略粒子初速度)求: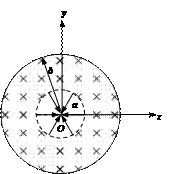
(1)粒子到达小圆周上时的速度为多大?
(2)粒子以(1)中的速度进入两圆间的磁场中,当磁感应强度超过某一临界值时,粒子将不能到达大圆周,求此最小值B。
(3)若磁感应强度取(2)中最小值,且b=(+1)a,要粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过多少次回旋?并求粒子在磁场中运动的时间。(设粒子与金属球正碰后电量不变且能以原速率原路返回)
伽利略在研究落体运动时,由于在短时间内物体下落的路程会很大,难于测量.为了“减慢”这个过程,伽利略设计了斜面滚球实验,测量从斜面上的光滑小槽内往下滚的青铜小球的位移与时间的关系.进一步证明他对落体运动中速度与时间关系的猜测:v∝t.如果设这个比例系数是a,请同学们据此推导落体运动的位移和时间的关系式.
简述频闪照片与打点计时器的记录原理.
请简要解释:为什么一张平整摊开的纸与同样大小揉成一团的纸,同时从同一高度的地方释放,下落的速度却不一样?
某物体以一定的初速度v0沿斜面向上运动,由实验测得物体沿斜面上升的最大位移s与斜面倾角θ的关系如图所示。若g取10m/s2,求:
(1)物体的初速度v0。
(2)物体与斜面之间的动摩擦因数μ。
(3)s最小时的θ角和s的最小值。
速度为24 m/s的火车,制动后20 s停止运动,求火车的加速度.