(本小题满分14分)已知函数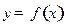 满足:
满足: ;(1)分别写出
;(1)分别写出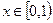 时
时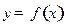 的解析式
的解析式 和
和 时
时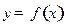 的解析式
的解析式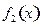 ;并猜想
;并猜想 时
时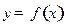 的解析式
的解析式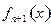 (用
(用 和
和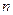 表示)(不必证明)(2)当
表示)(不必证明)(2)当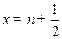
 时,
时,
 的图象上有点列
的图象上有点列 和点列
和点列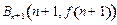 ,线段
,线段 与线段
与线段 的交点
的交点 ,求点
,求点 的坐标
的坐标 ;
;
(3)在前面(1)(2)的基础上,请你提出一个点列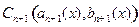 的问题,并进行研究,并写下你研究的过程
的问题,并进行研究,并写下你研究的过程
已知函数 .
.
(1)求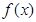 的单调区间;
的单调区间;
(2)当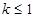 时,求证:
时,求证: 恒成立..
恒成立..
如图1,在Rt△ABC中,∠ABC=90°,D为AC中点,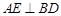 于
于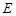 (不同于点
(不同于点 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥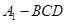 ,如图2所示.
,如图2所示.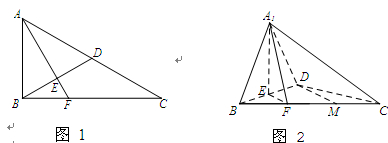
(1)若M是FC的中点,求证:直线 //平面
//平面 ;
;
(2)求证:BD⊥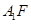 ;
;
(3)若平面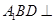 平面
平面 ,试判断直线
,试判断直线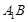 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由.
某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:
| 答对题目数 |
 |
8 |
9 |
 |
| 女 |
2 |
13 |
12 |
8 |
| 男 |
3 |
37 |
16 |
9 |
(1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(2)从答对题目数少于8的出租车司机中任选出两人做进一步的调查,求选出的两人中至少有一名女出租车司机的概率.
已知函数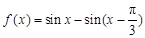 .
.
(1)求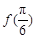 ;
;
(2)求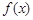 在
在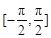 上的取值范围.
上的取值范围.
设不等式组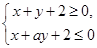 表示的区域为
表示的区域为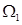 ,不等式
,不等式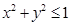 表示的平面区域为
表示的平面区域为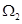 .
.
(1)若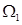 与
与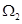 有且只有一个公共点,则
有且只有一个公共点,则 =;
=;
(2)记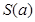 为
为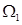 与
与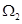 公共部分的面积,则函数
公共部分的面积,则函数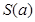 的取值范围是.
的取值范围是.