(本小题满分14分)已知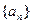 的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且
的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且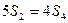 . (1)求q的值; (2)设
. (1)求q的值; (2)设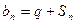 ,请判断数列
,请判断数列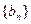 能否为等比数列,若能,请求出a1的值,否则请说明理由.
能否为等比数列,若能,请求出a1的值,否则请说明理由.
(本小题满分12分)
设等比数列 的前
的前 项和为
项和为 ,已知
,已知
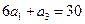 求
求 和
和 .
.
(本小题满分12分 ,要求画图规范)
用平面区域表示不等式组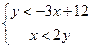 的解集.
的解集.
(本小题满分12分)已知函数 (
( ),其中
),其中 .
.
(Ⅰ)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(Ⅱ)若函数 仅在
仅在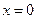 处有极值,求
处有极值,求 的取值范围;
的取值范围;
(Ⅲ)若对于任意的 ,不等式
,不等式 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)已知 ,
, ,若动点
,若动点 满足
满足 ,
, 点的轨迹为曲线
点的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)试确定 的取值范围,使得对于直线
的取值范围,使得对于直线 :
: ,曲线
,曲线 上总有不同的两点关于直线
上总有不同的两点关于直线 对称.
对称.
(本小题满分12分)已知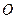 是边长为
是边长为 的正方形
的正方形 的中心,点
的中心,点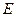 、
、 分别是
分别是 、
、 的中点,沿对角线
的中点,沿对角线 把正方形
把正方形 折成直二面角
折成直二面角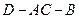 ;
;
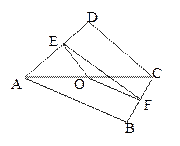
(Ⅰ)求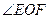 的大小;
的大小;
(Ⅱ)求二面角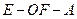 的余弦值;
的余弦值;
(Ⅲ)求点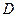 到面
到面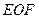 的距离.
的距离.