如图所示，相距2L的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场，其中PT上方的电场E1的场强方向竖直向下，PT下方的电场E0的场强方向竖直向上，在电场左边界AB上宽为L的PQ区域内，连续分布着电量为＋q、质量为m的粒子。从某时刻起由Q到P点间的带电粒子，依次以相同的初速度v0沿水平方向垂直射入匀强电场E0中，若从Q点射入的粒子，通过PT上的某点R进入匀强电场E1后从CD边上的M点水平射出，其轨迹如图，若MT两点的距离为L/2。不计粒子的重力及它们间的相互作用。试求：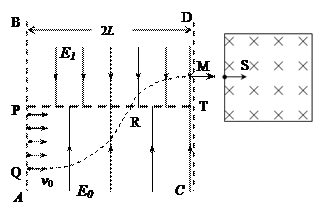
（1）电场强度E0与E1；
（2）在PQ间还有许多水平射入电场的粒子通过电场后也能垂直CD
边水平射出，这些入射点到P点的距离有什么规律？
（3）有一边长为a、由光滑绝缘壁
围成的正方形容器，在其边界正中
央开有一小孔S，将其置于CD右
侧，若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无能量和电量损失)，并返回Q点，在容器中现加上一个如图所示的匀强磁场，粒子运动的半径小于a，磁感应强度B的大小还应满足什么条件？
如图所示，质量M = 8kg的小车放在水平光滑的平面上，在小车左端加一水平恒力F，F = 8N，当小车向右运动的速度达到1.5m/s时，在小车前端轻轻地放上一个大小不计，质量为m = 2kg的小物块，物块与小车间的动摩擦因数μ = 0.2，小车足够长。取g = 10m/s2，求从小
物块放上小车开始，
（1）小物块运动的加速度是多少？小车运动的加速度变为多少？
（2）当小车和小物块获得共同速度时，共同速度多大？
（3）经过t =1.5s小物块通过的位移大小为多少？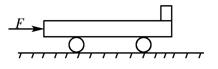 
一种巨型娱乐器械由升降机送到离地面75m的高处，然后让座舱自由落下。落到离地面25 m高时，制动系统开始启动，座舱均匀减速，到地面时刚好停下。若座舱中某人用手托着重50N的铅球，取g=10m/s2，试求：
（1）从开始下落到最后着地经历的总时间多长？
（2）当座舱落到离地面35m的位置时，手对球的支持力是多少？
（3）当座舱落到离地面15m的位置时，球对手的压力是多少？
如图9
所示，一光滑大圆环固定在竖直平面内，环上套着两个小球A和B（中央有孔），A、B间由细绳连接着，它们处于图中所示位置时恰好都能保持静止状态。此情况下，B球与环中心O处于同一水平面上，A、B间的细绳呈伸直状态，与水平线成30°夹角。已知B球的质量为m，求：
（1）细
绳对B球的拉力？
（2）A球的质量？
一上表面光滑，质量为M =" 10" kg足够长的长木板，在F =" 50" N的水平拉力作用下，恰好沿着水平地面做匀速直线运动且速度为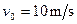
（如图一）。现每隔
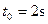将质量为m =" 0.5" kg铁片无初速地置于木板上，放上第一块铁片时，记为时刻t = 0，直到木板静止（静止后不再继续放铁片）。取
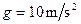，求：
(1)放上第一块铁片后（放第二块铁片前）木板加速度的大小；
(2)木板上最多放的铁片数；
(3)试在图二中画出木板加速度的大小随时间t变化的图象（至少画出0至8 s内图象）。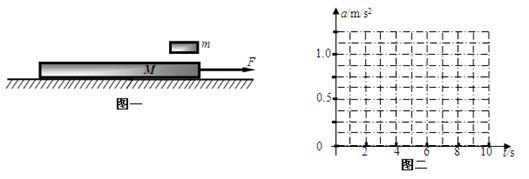
在一次摩托车跨越壕沟的表演中，摩托车从壕沟的一侧以速度
沿水平方向飞向另一侧，壕沟的宽度及两侧的高度如图所示（不计空气阻力，取g =" 10" m/s2，可能用到的三角函数值为sin30°= 0.50、sin37°= 0.60、sin45°= 0.71、sin60°= 0.87、sin90° = 1.0）。
（1）摩托车是否能越过壕沟？请计算说明。
（2）摩托车如果能越过壕沟，它落地时的速度是多大？与水平方向的夹角如何？