(本小题满分14分)已知: 为常数)
为常数)
(1)若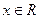 ,求
,求 的最小正周期;(2)若
的最小正周期;(2)若 在[
在[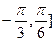 上最大值与最小值之和为5,求
上最大值与最小值之和为5,求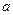 的值;(3)在(2)条件下
的值;(3)在(2)条件下 先按
先按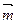 平移后再经过伸缩变换后得到
平移后再经过伸缩变换后得到 求
求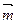 .
.
(本小题満分12分)设p :指数函数 在R上是减函数;q:
在R上是减函数;q: 。若p∨q是真命题,p∧q是假命题,求
。若p∨q是真命题,p∧q是假命题,求 的取值范围。
的取值范围。
如果正△ABC中,D∈AB,E∈AC,向量 ,求以B,C为焦点且过点D,E的双曲线的离心
,求以B,C为焦点且过点D,E的双曲线的离心
(本小题满分14分)一块边长为10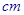 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积 与
与 的函数关系式,并求出函数的定义域.
的函数关系式,并求出函数的定义域.
(本小题满分14分)
如图所示,在长方体 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M1
(本小题满分14分)
已知圆C: ,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在,求出直线l的方程;若不存在说明理由。
,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在,求出直线l的方程;若不存在说明理由。