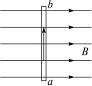
光滑水平面上放着质量,1kg的物块A与质量2kg的物块,与均可视为质点,靠在竖直墙壁上,、间夹一个被压缩的轻弹簧(弹簧与、均不拴接),用手挡住不动,此时弹簧弹性势能49J。在、间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示。放手后向右运动,绳在短暂时间内被拉断,之后冲上与水平面相切的竖直半圆光滑轨道,其半径0.5m, B恰能到达最高点。取10m/s2,求:

(1)绳拉断后瞬间的速度的大小;
(2)绳拉断过程绳对的冲量 的大小;
(3)绳拉断过程绳对所做的功。
如图15-3-12所示的磁电式电流表的内部示意图.已知辐射状磁场的磁感应强度B="0.9" T,矩形线圈边长L1="2" cm,L2="2.5" cm,匝数N="2" 000,电流表的满偏角为θ=90°,与线圈相连的两个螺旋弹簧总的扭转特征是:每扭转1°,产生的力矩为1×10-6 N·m.求该电流表的满偏电流.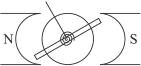
图15-3-12
设电流计中的磁场为均匀辐向分布的磁场,如图(乙)中abcd表示的是电流计中的通电线圈.ab="cd=1" cm,ad="bc=0.9" cm,共有50匝,线圈两边所在位置的磁感应强度为0.5 T.已知线圈每偏转1°,弹簧产生的阻碍线圈偏转的力矩为2.5×10-8 N·m.求:
(1)当线圈中通有0.6 mA的电流时,线圈偏转的角度;
(2)当线圈转过90°时,该电流表中通过的电流.
如图所示,在倾角为30°的光滑斜面上,垂直纸面放置着一通电导线,导线长为L,质量为m,其中的电流为I,方向垂直纸面向外.
(1)若加一垂直斜面向上的匀强磁场,使导线棒在斜面上保持静止,求磁场的磁感应强度.
(2)若加一垂直水平面向上的匀强磁场,使导线棒在斜面上保持静止,求磁场的磁感应强度.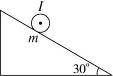
用细绳将一根长为50 cm、质量为10 g的直导线MN平挂在磁感应强度为1.0 T的磁场中,导线中通有电流I,电流的方向和磁场垂直,如图所示.要使细绳的张力为零,则导线中的电流大小是多少?方向如何?
在磁感应强度是4.0×10-2 T的匀强磁场中,有一条与磁场方向垂直的导线ab,导线长为8 cm,通有2.5 A的电流,方向由a到b,如图所示.试求导线所受安培力的大小和方向.