磁悬浮列车是一种高速低耗的新型交通工具,它的驱动系统简化为如下模型,固定在列车下端的动力绕组可视为一个矩形纯电阻金属框,电阻为,金属框置于平面内,长边为平行于轴,宽为的边平行于轴,如图l所示。列车轨道沿方向,轨道区域内存在垂直于金属框平面的磁场,磁感应强度沿方向按正弦规律分布,其空间周期为,最大值为,如图2所示,金属框同一长边上各处的磁感应强度相同,整个磁场以速度沿方向匀速平移。设在短暂时间内,、边所在位置的磁感应强度随时问的变化可以忽略,并忽略一切阻力。列车在驱动系统作用下沿方向加速行驶,某时刻速度为

()
(1)简要叙述列车运行中获得驱动力的原理;
(2)为使列车获得最大驱动力,写出、边应处于磁场中的什么位置及与之间应满足的关系式;
(3)计算在满足第(2)问的条件下列车速度为v时驱动力的大小。
如图7-5-16所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=5.0 m,轨道在C处与水平地面相切.在C处放一小物块,给它一水平向左的初速度v0=5 m/s,结果它沿CBA运动,通过A点,最后落在水平面上的D点,求C、D间的距离s.取重力加速度g=10 m/s2.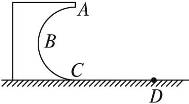
图7-5-16
如图7-5-14所示,矿井深100 m,用每米质量为1 kg的钢索把质量为100 kg的机器从井底提到井口,至少应该做多少功?(机器可视为质点,取g=10m/s2)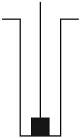
图7-5-14
面积很大的水池,水深为H,水面上浮着一正方体木块,木块边长为a,密度为水的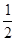 ,质量为m.开始时,木块静止,有一半没入水中,如图7-5-11所示,现用力F将木块缓慢地压到池底,不计摩擦.求:从木块刚好完全没入水中到停止在池底的过程中,池水势能的改变量.
,质量为m.开始时,木块静止,有一半没入水中,如图7-5-11所示,现用力F将木块缓慢地压到池底,不计摩擦.求:从木块刚好完全没入水中到停止在池底的过程中,池水势能的改变量.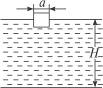
图7-5-11
如图7-5-8所示,轻质绳子绕过光滑的定滑轮,它的一端拴住一个质量为10 kg的物体,人竖直向下拉绳子,使物体处于静止状态,AB长4 m,然后人拉着绳子的一端沿水平方向缓慢地由A移到C,A、C相距3 m.在这个过程中人做的功是多少?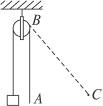
图7-5-8
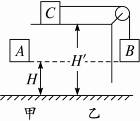
如图所示,甲图中物体A从高H处由静止开始下落.乙图中物体B与C通过光滑轻滑轮用细绳相连,C放在光滑水平桌面上,C的质量是B的一半,物体B也从H高处由静止下落.求这两种情况下,A、B离地面的高度h为多少时,其动能等于势能?(设C尚未离开桌面)